Kezdőlap


Feladat:	B.4870	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csahók Tímea
Füzet:	2017/szeptember, 350 - 352. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Feuerbach-kör, Konvex négyszögek
Hivatkozás(ok):	Feladatok: 2017/április: B.4870

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mivel egy háromszög Feuerbach-körének középpontja a körülírt köre középpontjának és magasságpontjának a szakaszfelező pontja, így vizsgáljuk meg ezeket a pontokat.
Jelölje az

A B E

B C E

C D E

A D E

háromszögek körülírt körének középpontját rendre

K_{1}

K_{2}

K_{3}

K_{4}

(1. ábra). Mivel egy háromszög körülírt körének középpontja az oldalfelezőinek a metszéspontja, így

K_{1} K_{2} ∥ K_{3} K_{4} ⊥ B D

és

K_{1} K_{4} ∥ K_{2} K_{3} ⊥ A C

, így mivel két párhuzamos oldalpárja van

K_{1} K_{2} K_{3} K_{4}

paralelogramma.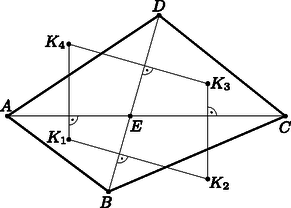

1. ábra

Legyenek a fenti háromszögek magasságpontjai rendre

M_{1}

M_{2}

M_{3}

M_{4}

(2. ábra). A magasságpont a csúcsokból a szemközti oldalakra állított merőlegesek metszéspontja, így

M_{1} M_{2} ∥ M_{3} M_{4} ⊥ A C

és

M_{1} M_{4} ∥ M_{2} M_{3} ⊥ B D

, tehát hasonlóan az előzőhöz

M_{1} M_{2} M_{3} M_{4}

is paralelogramma.

2. ábra

Legyen

\vec{K_{1} K_{2}} = \vec{k_{1}}

\vec{K_{3} K_{4}} = \vec{k_{3}}

\vec{M_{1} M_{2}} = \vec{m_{1}}

\vec{M_{3} M_{4}} = \vec{m_{3}}

. Mivel

K_{1} K_{2} K_{3} K_{4}

és

M_{1} M_{2} M_{3} M_{4}

paralelogramma, így tudjuk, hogy

\vec{k_{1}} = - \vec{k_{3}}

és

\vec{m_{1}} = - \vec{m_{3}}

. Mivel

K_{1} M_{1} {K_{2} M}_{2}

négyszögben

F_{1} F_{2}

középvonal (3. ábra), ezért tudjuk, hogy

\begin{matrix} \vec{F_{1} F_{2}} = \vec{f_{1}} = \frac{\vec{k_{1}} + \vec{m_{1}}}{2} \end{matrix}

Valamint hasonlóan a

K_{3} M_{3} {K_{4} M}_{4}

négyszögben

\begin{matrix} \vec{F_{3} F_{4}} = \vec{f_{3}} = \frac{\vec{k_{3}} + \vec{m_{3}}}{2} = \frac{- (\vec{k_{1}} + \vec{m_{1}})}{2} = - \vec{f_{1}} . \end{matrix}

3. ábra

Tehát

\vec{f_{3}} = - \vec{f_{1}}

, így

F_{1} F_{2} ∥ F_{3} F_{4}

és egyenlő hosszúak, vagyis

F_{1} F_{2} F_{3} F_{4}

valóban paralelogramma, vagy a négy pont egy egyenesre esik. Ezt kellett bizonyítani.