Kezdőlap


Feladat:	B.4819	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Török Emese
Füzet:	2017/április, 219 - 220. oldal		PDF \| MathML
Témakör(ök):	Feladat, Trigonometrikus egyenlőtlenségek, Exponenciális függvények, Számtani-mértani egyenlőtlenségek
Hivatkozás(ok):	Feladatok: 2016/október: B.4819

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mivel $0 < x < \frac{π}{2}$ , az egyenlőtlenség szögfüggvényeit felírhatjuk az $A B C$ derékszögű háromszög $x$ hegyesszögének szögfüggvényeiként: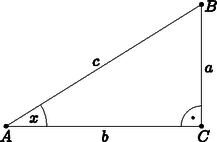

\begin{matrix} sin x = \frac{a}{c}, cos x = \frac{b}{c}, tg x = \frac{a}{b}, ctg x = \frac{b}{a} . \end{matrix}

Ezek felhasználásával a bizonyítandó egyenlőtlenség:

\begin{matrix} {(\frac{a}{b})}^{\frac{a}{c}} + {(\frac{b}{a})}^{\frac{b}{c}} \geq 2. \end{matrix}

Bármely

p

q

pozitív valós számra igaz a számtani és mértani középre vonatkozó egyenlőtlenség:

\begin{matrix} \frac{p + q}{2} \geq \sqrt[]{p q} . \end{matrix}

A háromszög oldalai pozitív számok, így

{(\frac{a}{b})}^{\frac{a}{c}}

és

{(\frac{b}{a})}^{\frac{b}{c}}

is azok.

Alkalmazzuk a számtani és mértani középre vonatkozó egyenlőtlenséget ezekre:

\begin{matrix} {(\frac{a}{b})}^{\frac{a}{c}} + {(\frac{b}{a})}^{\frac{b}{c}} \geq 2 \cdot \sqrt[]{{(\frac{a}{b})}^{\frac{a}{c}} \cdot {(\frac{b}{a})}^{\frac{b}{c}}} . \end{matrix}

A négyzetgyökjel alatti kifejezést átalakítva:

\begin{matrix} {(\frac{a}{b})}^{\frac{a}{c}} \cdot {(\frac{b}{a})}^{\frac{b}{c}} = {(\frac{a}{b})}^{\frac{a}{c}} \cdot {(\frac{a}{b})}^{- \frac{b}{c}} = {(\frac{a}{b})}^{\frac{a - b}{c}} . \end{matrix}

Ezzel

\begin{matrix} {(\frac{a}{b})}^{\frac{a}{c}} + {(\frac{b}{a})}^{\frac{b}{c}} \geq 2 \cdot \sqrt[]{{(\frac{a}{b})}^{\frac{a - b}{c}}} . \end{matrix}

a > b

, akkor

\frac{a}{b} > 1

és

\frac{a - b}{c} > 0

, így

\begin{matrix} \sqrt[]{{(\frac{a}{b})}^{\frac{a - b}{c}}} > 1, tehát {(\frac{a}{b})}^{\frac{a}{c}} + {(\frac{b}{a})}^{\frac{b}{c}} > 2. \end{matrix}

a < b

, akkor

\begin{matrix} {(\frac{a}{b})}^{\frac{a - b}{c}} = {(\frac{b}{a})}^{- \frac{a - b}{c}} = {(\frac{b}{a})}^{\frac{b - a}{c}} . \end{matrix}

Mivel

\frac{b}{a} > 1

és

\frac{b - a}{c} > 0

, emiatt

\begin{matrix} \sqrt[]{{(\frac{b}{a})}^{\frac{b - a}{c}}} > 1, tehát {(\frac{a}{b})}^{\frac{a}{c}} + {(\frac{b}{a})}^{\frac{b}{c}} > 2. \end{matrix}

a = b

, akkor

x = 45^{\circ}

, ezért

tg x = ctg x = 1

, tehát

1^{\frac{a}{c}} + 1^{\frac{b}{c}} = 2