Feladat:	B.4539	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Badacsonyi István András ,  Balogh Tamás ,  Bereczki Zoltán ,  Bingler Arnold ,  Bogár Blanka ,  Di Giovanni Márk ,  Dinev Georgi ,  Emri Tamás ,  Fonyó Viktória ,  Forrás Bence ,  Janzer Barnabás ,  Janzer Olivér ,  Maga Balázs ,  Makk László ,  Petrényi Márk ,  Sándor Krisztián ,  Sárosdi Zsombor ,  Simkó Irén ,  Somogyvári Kristóf ,  Szabó Tímea ,  Tossenberger Tamás ,  Venczel Tünde
Füzet:	2015/május, 274 - 275. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Súlyvonal, Körülírt kör, Hatványvonal, hatványpont
Hivatkozás(ok):	Feladatok: 2013/április: B.4539

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. A $PQR$ háromszög oldalai az $SA$, $SB$, $SC$ szakaszok felezőmerőlegesei. Elegendő megmutatni, hogy az $ABC$ háromszög oldalfelező merőlegesei a $PQR$ háromszög súlyvonalai, hiszen ekkor a három egyenes közös $K$ pontja a $PQR$ háromszög súlypontja lesz. Ezt szimmetria okok miatt elég egy felezőmerőlegesre bizonyítani. Jelölje az oldalak felezőpontjait az ábra szerint $A_0$, $B_0$ és $C_0$, valamint $PQ$-nak és $AB$ felezőmerőlegesének metszéspontját $T$. Ha megmutatjuk, hogy $T$ felezi a PQ szakaszt, akkor bebizonyítottuk az állítást. Vetítsük a $PQ$ szakaszt merőlegesen $AB$-re, $P$ és $Q$ képe legyen rendre $E$, illetve $D$. $T$ képe nyilván $C_0$, amivel $AB$ felezőpontját jelöltük. Amennyiben $T$ felezőpont, $C_0$ felezi $ED$-t is, amiből $AD=EB$. Megfordítva: ha ez igaz, a feladat állítása is igaz. 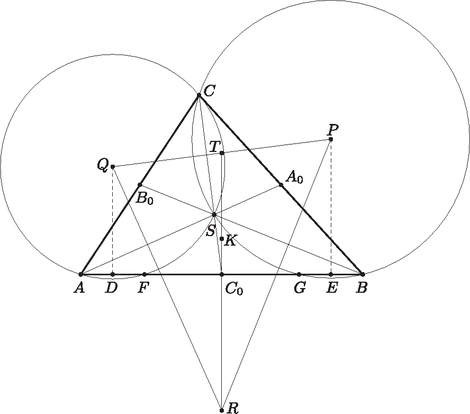    A $CS$ egyenes az $ACS$ és $BCS$ háromszögek köré írt körök közös húrja, vagyis hatványvonala. Emiatt $C_0$-nak a két körre vonatkozó hatványa ugyanakkora, vagyis a körök $AB$-vel vett második metszéspontját $G$-vel és $F$-el jelölve: $\begin{array}{c}{\displaystyle C_{0}F\cdot C_{0}A=C_{0}G\cdot C_{0}B\mathrm{.}}\end{array}$ Mivel $C_{0}A=C_{0}B\ne 0$, leoszthatunk vele. Azt kapjuk, hogy $C_{0}F=C_{0}G$. Mivel $C_0$ felezőpont, ebből következik, hogy $AF=BG$. $AF$ és $BG$ rendre az $ACS$, illetve $BCS$ körök húrjai, így a $D$ és $E$ pontok felezik őket (mivel középpontból húrra bocsátott merőlegesek talppontjai). Tehát az $AF=BG$ egyenlőséget kettővel osztva kapjuk, hogy $AD=EB$. Ezzel pedig bebizonyítottuk az állítást.