| Feladat: | B.4215 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bogár Blanka | ||
| Füzet: | 2010/szeptember, 341. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Húrnégyszögek, Külső szög tétel, Síkgeometriai bizonyítások | ||
| Hivatkozás(ok): | Feladatok: 2009/november: B.4215 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Feltehetjük, hogy és különböző pontok (ellenkező esetben az pont nem meghatározott, de persze bármely lehetséges helyzetére igaz, hogy a négy pont egy körön helyezkedik el), és azt is, hogy az egyenes nem merőleges -re, ellenkező esetben ugyanis az pont nem létezik (bár felfogható egy végtelen távoli pontnak, amely az egyenessé fajuló végtelen sugarú körön helyezkedik el). Ha párhuzamos -vel, akkor az és az pont egybeesik, ezért az állítás nyilvánvaló. A fennmaradó esetekben, mivel egyik pontnak sincs kitüntetett szerepe, feltehetjük, hogy közelebb van -hez, mint . 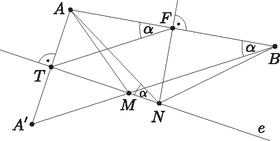 Jelölje felezőpontját . Ekkor az négyszög húrnégyszög, mert -nél és -nél lévő szögei derékszögek. Ezért , mert mindkettő az négyszög köré írt körének rövidebbik ívéhez tartozó kerületi szög. Az és az , illetve szakaszok felezőpontjai, ezért az és háromszögek hasonlóak, tehát . Tehát az szakasz -ből és -ből ugyanakkora szögben látszik. Az közelebb van -hez, mint , ezért , vagyis és az egyenesnek ugyanazon az oldalán helyezkedik el. Tehát és az szakasz szöghöz tartozó két látóköríve közül ugyanazon van rajta. Így az négyszög valóban húrnégyszög. |