Kezdőlap


Feladat:	B.4307	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Mihálykó András
Füzet:	2011/november, 475 - 476. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai bizonyítások, Indirekt bizonyítási mód, Feladat
Hivatkozás(ok):	Feladatok: 2010/november: B.4307

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A háromszög területe legyen egységnyi, a négy pontot pedig jelölje $P$ , $Q$ , $R$ , $S$ az ábra szerint.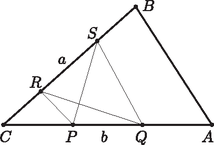

Legyen továbbá

C P = p \cdot A C

Q C = q \cdot A C

0 < p < q < 1

és

C R = r \cdot B C

C S = s \cdot B C

0 < r < s < 1

. Ekkor

P Q = x \cdot A C

és

R S = = y \cdot B C

, ahol

0 < x = q - p < 1 - p

, valamint

0 < y = s - r < 1 - r

.
A

P Q R

háromszög területe (mivel

A B C

területét egységnyinek választottuk):

\begin{matrix} T_{P Q R} & = T_{Q R C} - T_{P R C} = \frac{1}{2} q \cdot A C \cdot r \cdot B C \cdot sin γ - \frac{1}{2} p \cdot A C \cdot r \cdot B C \cdot sin γ = \\ = (q r - p r) \frac{1}{2} A C \cdot B C \cdot sin γ = (q - p) r < (1 - p) r . \end{matrix}

Hasonlóan kapjuk az

R S P

háromszög területére

\begin{matrix} T_{R S P} & = T_{S P C} - T_{P R C} = \frac{1}{2} s \cdot B C \cdot p \cdot A C \cdot sin γ - \frac{1}{2} p \cdot A C \cdot r \cdot B C \cdot sin γ = \\ = (s p - r p) \frac{1}{2} A C \cdot B C \cdot sin γ = (s - r) p < (1 - r) p . \end{matrix}

Elegendő megmutatni, hogy valamelyik nem nagyobb

1 / 4

-nél. Ha mindkettő nagyobb lenne, mint

1 / 4

, akkor négyzetgyökvonás után a számtani-mértani középre vonatkozó egyenlőtlenség alkalmazásával

\begin{matrix} 1 & = \frac{1}{2} + \frac{1}{2} < \sqrt[]{(1 - p) r} + \sqrt[]{(1 - r) p} \leq \\ \leq \frac{1 - p + r}{2} + \frac{1 - r + p}{2} = \frac{2 - p + r - r + p}{2} = 1. \end{matrix}

Ellentmondásra jutottunk, tehát legalább az egyik terület biztosan nem nagyobb, mint

1 / 4

. Ha a

P

és

R

pontokat az

A C

, illetve a

B C

oldalak felezőpontjának választjuk, továbbá

Q \equiv A

és

S \equiv B

, akkor látható az is, hogy a feladat állítása nem javítható.