Kezdőlap


Feladat:	B.4229	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bogár Blanka
Füzet:	2010/május, 286. oldal		PDF \| MathML
Témakör(ök):	Feladat, Másodfokú (és arra visszavezethető) egyenletrendszerek, Húrnégyszögek, Körülírt kör, Koszinusztétel alkalmazása
Hivatkozás(ok):	Feladatok: 2009/december: B.4229

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Az ábra jelöléseit használva az $A C$ átló $A$ -hoz közelebbi harmadolópontja legyen $H$ , a paralelogramma oldalai 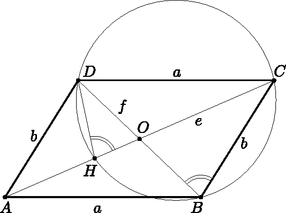$a$ és $b$ , átlói $e$ és $f$ .

Alkalmazzuk az ismert azonosságot, mely szerint a paralelogrammában az oldalak négyzetösszege egyenlő az átlók négyzetösszegével:

\begin{matrix} 2 a^{2} + 2 b^{2} = e^{2} + f^{2} . \end{matrix}

A feladat feltétele pedig:

2 f^{2} = a^{2} + b^{2}

, azaz

4 f^{2} = 2 a^{2} + 2 b^{2}

. Ezt behelyettesítve az előző egyenletbe:

4 f^{2} = e^{2} + f^{2}

, vagyis

3 f^{2} = e^{2}

. Alakítsuk át ezt az összefüggést:

\begin{matrix} \frac{f^{2}}{4} = \frac{e^{2}}{12} \Rightarrow \frac{\frac{f}{2}}{\frac{e}{6}} = \frac{\frac{e}{2}}{\frac{f}{2}} . \end{matrix}

Mivel

\frac{f}{2} = O D

\frac{e}{2} = O A

és

\frac{e}{6} = O H

, azért

\begin{matrix} \frac{O D}{O H} = \frac{O A}{O D} . \end{matrix}

Látható, hogy

D O H ∢ = D O A ∢

, ezért

O D H ▵ \sim O A D ▵

, mert két oldaluk aránya és a közbezárt szög megegyezik. Ebből következik, hogy harmadik szögük is megegyezik:

A D O ∢ = D H O ∢

.
Nyilván

A D O ∢ = D B C ∢

, így

D H O ∢ = D B C ∢

. Tehát a

D C

oldal a

H

és

B

pontokból ugyanakkora szög alatt látszik, így a

H

pontnak rajta kell lennie a

D B C ▵

köré írt körén. Ezzel az állítást bebizonyítottuk.