| Feladat: | B.3947 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Füzet: | 2008/május, 279. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai bizonyítások, Pont körre vonatkozó hatványa, Körülírt kör, Thalesz tétel és megfordítása, Feladat | ||
| Hivatkozás(ok): | Feladatok: 2006/november: B.3947 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Az érintési pontok által meghatározott hosszabbik köríven rögzített ponthoz keressük meg a körön azokat a pontokat, amelyekre . Az érintő és szelő szakaszok tétele miatt egy ilyen pont , ami a egyenesnek a körrel alkotott másik metszéspontja. Tudjuk továbbá, hogy a síkon a megfelelő pontok egy középpontú ( sugarú) körön vannak. Így a keresett pontok , és a tengelyre vonatkozó tükörképe, . Belátjuk, hogy átmegy az ponton. Mivel az és szakaszok metszéspontja, azt kell megmutatnunk, hogy , és egy ponton mennek át. Ez azért igaz, mert van három kör, amelyeknek ezek a szakaszok a páronként közös húrjaik, vagyis a hatványvonalaik. Az pedig ismert tény, hogy a hatványvonalak egy ponton mennek át (a három kör hatványpontján). Ezek a körök az eredeti kör, a szakasz Thalesz-köre és a négyszög körülírt köre. A négyszög azért húrnégyszög, mert -ból és -ból a szakasz egyaránt fele akkora szög alatt látszik, mint amekkora a középponti szög. 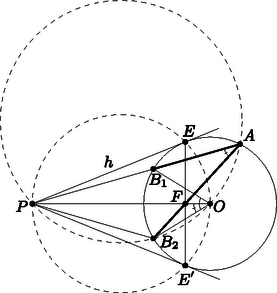 Ennek alapján a tétel két irányának bizonyítása: Ha fennáll , akkor és valamelyike a hosszabb köríven van, mert különben mindkettő -nál közelebb lenne -hez. Erre a pontra mint ,,''-ra alkalmazva a föntieket kapjuk, hogy átmegy -n vagy -en. Megfordítva: ha átmegy -n vagy -en, akkor és valamelyike a hosszabb köríven van. Erre mint ,,''-ra alkalmazva a föntieket adódik, hogy . |