Kezdőlap


Feladat:	B.3837	Korcsoport: 14-15	Nehézségi fok: nehéz
Füzet:	2006/február, 95 - 96. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Négyzetek, Háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 2005/szeptember: B.3837

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelölje az $A B$ szakasz felezőpontját $F$ , a $B C$ -ét $I$ , a $B D$ -ét $J$ , a $B H$ -ét pedig $K$ . Mivel $P J B F$ négyzet, $P J$ párhuzamos és egyenlő az $A B C$ háromszög $R I$ középvonalával; hasonlóan $J S$ párhuzamos és egyenlő $I Q$ -val. Ezért (azonos körüljárásuk miatt) a $P J S$ háromszög az $R I Q$ háromszög eltoltja, így $P S$ párhuzamos és egyenlő az $R Q$ szakasszal. Ugyanígy adódik, hogy $S Q$ párhuzamos és egyenlő $P R$ -rel. A feladat megoldásához már csak azt kell megmutatni, hogy például a $P S$ és a $P R$ szakaszok egyenlők és egymásra merőlegesek. Forgassuk el ehhez a $P J S$ háromszöget $P$ körül $90^{\circ}$ -kal, így a $J$ pont $F$ -be kerül. Mivel $J S$ a $D B H$ háromszög $B H$ oldalához tartozó középvonala, $J S$ párhuzamos és egyenlő $B K$ -val. Az $R F$ szakasz viszont az $A B C$ háromszög $B C$ oldalához tartozó középvonala, ezért $R F$ párhuzamos és egyenlő $B I$ -vel. A $B I$ és $B K$ szakaszok a $B K Q I$ négyzet szomszédos oldalai lévén merőlegesek és egyenlő hosszúságúak, ezért ugyanez teljesül a $J S$ és $F R$ szakaszokra is. Tehát (azonos körüljárásuk miatt) a $P J S$ háromszöget $P$ körül $90^{\circ}$ -kal elforgatva a $P F R$ háromszöghöz jutunk, ezen belül $P S$ a $P R$ -be kerül. Ezzel állításunkat beláttuk.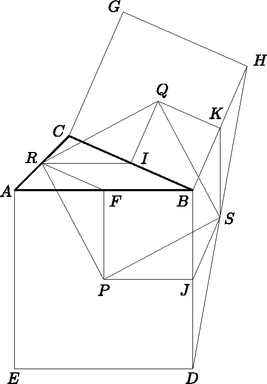

II. megoldás. A feladat (és sok, ehhez hasonló kérdés) a komplex számok segítségével szinte gépiesen, bár némi számolással megoldható. Tekintsük ehhez a sík egy tetszőlegesen rögzített

O

pontját, és a belőle a sík különböző pontjaiba mutató vektorokat azonosítsuk a komplex számokkal. Jelöljük általában az

\vec{O P}

vektort, illetve a neki megfelelő komplex számot

p

-vel. A számolás alapja egyrészt a komplex számok körében az alapműveletekre vonatkozó műveleti azonosságok teljesülése, másrészt az, hogy az

i

-vel való szorzás az

O

körüli

90^{\circ}

-os forgatásnak felel meg. A korábbi jelölésekkel ekkor

\begin{matrix} \vec{P S} & = & s - p = \frac{1}{2} (h + d) - (f + \vec{F P}) = \frac{1}{2} ((b + \vec{B H}) + (b + \vec{B D})) - (f + i \cdot \vec{F A}) = \\ = & \frac{1}{2} ((b + i (b - c)) + (b + i (a - b))) - (\frac{1}{2} (a + b) + i \frac{1}{2} (a - b)) = \\ = & \frac{1}{2} (- a + b (i + 1) - c i), \\ \vec{S Q} & = & q - s = (\frac{1}{2} (b + c) + i \frac{1}{2} (b - c)) - \frac{1}{2} ((b + i (b - c)) + (b + i (a - b))) = \\ = & \frac{1}{2} (- a i + b (i - 1) + c), \\ \vec{Q R} & = & r - q = \frac{1}{2} (a + c) - (\frac{1}{2} (b + c) + i \frac{1}{2} (b - c)) = \frac{1}{2} (a - b (i + 1) + c i) . \end{matrix}

Látható, hogy

\begin{matrix} \vec{P S} \cdot i & = & \frac{1}{2} (- a + b (i + 1) - c i) i = \frac{1}{2} (- a i + b (- 1 + i) + c) = \vec{S Q}, \\ \vec{S Q} \cdot i & = & \frac{1}{2} (- a i + b (i - 1) + c) \cdot i = (a + b (- 1 - i) + c i) = \vec{Q R} . \end{matrix}

Tehát

P S

90^{\circ}

-os elforgatottja

S Q

, az

S Q

90^{\circ}

-os elforgatottja

Q R

, azaz

P S Q R

valóban négyzet.