Kezdőlap


Feladat:	B.3574	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Juhász Máté Lehel
Füzet:	2003/május, 281 - 282. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül, Pont körre vonatkozó hatványa, Középpontos és egyéb hasonlósági transzformációk, Feladat
Hivatkozás(ok):	Feladatok: 2002/október: B.3574

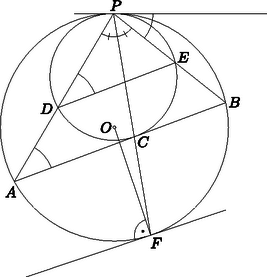
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel a két kör $P$ -nél levő érintője közös, $P D E ∢ = P A B ∢$ , hiszen a megfelelő körökben ahhoz az ívhez tartozó kerületi szögek, amelyhez a $P$ -nél keletkező érintőszárú kerületi szög is tartozik (ábra).

A B P

és

D E P

háromszögek hasonlósága miatt így

\begin{matrix} P A : P B = P D : P E = 11 : 10, \end{matrix}

vagyis

\begin{matrix} P A = \frac{11}{10} P B és P D = \frac{11}{10} P E . \end{matrix}

Ezért a szelőtétel szerint

\begin{matrix} \frac{A C^{2}}{B C^{2}} = \frac{A P \cdot A D}{B P \cdot B E} = \frac{P A (P A - P D)}{P B (P B - P E)} = \frac{\frac{11}{10} P B \cdot (\frac{11}{10} P B - \frac{11}{10} P E)}{P B (P B - P E)} = \frac{11^{2}}{10^{2}}, \end{matrix}

azaz

B C = \frac{10}{11} A C

. Innen

84 = A B = A C + B C = \frac{21}{11} A C

, tehát

A C = \frac{11}{21} \cdot 84 = 44

II. megoldás. Alkalmazzuk azt a

P

középpontú nagyítást, amely a kisebbik kört a nagyobbikba viszi. Ennek során

D

képe

A

E

képe

B

, így

\begin{matrix} P A : P B = P D : P E = 11 : 10. \end{matrix}

A B

egyenes képe párhuzamos

A B

-vel, és érinti a nagyobbik kört; jelölje az érintési pontot

F

. Az

F

pont felezi az

A B

ívet, hiszen az érintő merőleges az érintési pontba húzott

O F

sugárra, ami ‐ merőleges lévén az érintővel párhuzamos

A B

húrra ‐ éppen az

A B

szakasz felező merőlegesén van. Így

P F

felezi az

A P B

szöget. Mivel

A B

C

-ben érinti a kisebbik kört, a nagyítás során

C

képe

F

, azaz

C

a szögfelezőre esik. A szögfelező tétel szerint

A C : C B = P A : P B = 11 : 10

, tehát

\begin{matrix} A C = \frac{11}{21} A B = \frac{11}{21} \cdot 84 = 44. \end{matrix}

() Juhász Máté Lehel (Budapest, Fazekas M. Főv. Gyak. Gimn., 11. évf.)