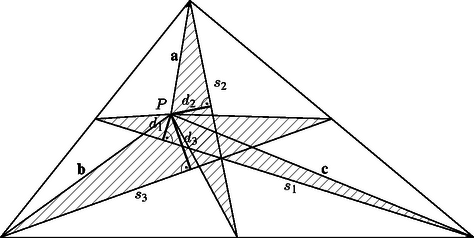
A feladatban szereplő $s_i{d}_i$ szorzatok éppen azon háromszögek területeinek kétszeresei, amely háromszögek egyik csúcsa $P$, azzal szemközti oldaluk pedig a kiindulási háromszög egyik súlyvonala. Tulajdonképpen azt kell megmutatnunk, hogy e három területet előjelezhetjük úgy, hogy az előjeles összegük 0 legyen.
Jelöljük a $P$-ből az eredeti háromszög csúcsaiba mutató vektorokat $\text{a}$, $\text{b}$, $\text{c}$-vel. Ekkor az oldalfelező pontokba mutató vektorok $\frac{\text{a}+\text{b}}{2}$, $\frac{\text{b}+\text{c}}{2}$ és $\frac{\text{c}+\text{a}}{2}$, s így $\frac{\text{a}+\text{b}}{2}\times \text{c}$, $\frac{\text{b}+\text{c}}{2}\times \text{a}$ és $\frac{\text{c}+\text{a}}{2}\times \text{b}$ olyan egymással párhuzamos vektorok, amelyek hossza valamilyen sorrendben $s_1{d}_1$, $s_2{d}_2$ és $s_3{d}_3$. Mivel bármilyen $\text{x}$ és $\text{y}$ vektorokra igaz, hogy $\text{x}\times \text{y}+\text{y}\times \text{x}=\text{0}$, ezért