Kezdőlap


Feladat:	671. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gajdics György , Gnädig Péter , Hegedüs Endre , Lánczos László , Szalay Sándor , Takács László
Füzet:	1967/december, 234 - 235. oldal		PDF \| MathML
Témakör(ök):	Newton-féle gravitációs erő, Egyenletes körmozgás, Mesterséges holdak, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1967/február: 671. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha $R$ távolságra tesszük a műholdat, akkor biztos, hogy nem ilyen pályát kapunk, mert a Hold vonzóereje is számít.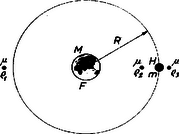
Mivel a feladat szövege csak a pálya egzisztenciája felől érdeklődik, ezért elég, ha egy speciális pályatípuson belül mutatunk példát. Keressünk tehát a mondott feltételeket kielégítő kör alakú pályát. Mivel körpályán a gyorsulás mindig sugárirányú, ezért a műhold csak a Föld és Hold középpontját összekötő egyenesen helyezkedhet el, mert csak így lesz a Holdból származó vonzóerő sugárirányú. A lehetséges elrendezések esetén (ábra) írjuk fel a Földtől $ϱ$ távolságra keringő műholdra $t$ időpillanatban ható erőket.

1. Ha a műhold és a Hold között van a Föld, akkor

\begin{matrix} F = \frac{f M μ}{ϱ^{2}} + \frac{f m μ}{{(R + ϱ)}^{2}} . \end{matrix}

2. Ha a Hold és a Föld között van a műhold, akkor

\begin{matrix} F = \frac{f M μ}{ϱ^{2}} - \frac{f m μ}{{(R - ϱ)}^{2}} . \end{matrix}

3. Ha a Föld és a műhold között van a Hold, akkor

\begin{matrix} F = \frac{f M μ}{ϱ^{2}} + \frac{f m μ}{{(R - ϱ)}^{2}} . \end{matrix}

F = m a

mozgásegyenlet alapján körpálya esetén

a = ϱ ω_{H}^{2}

, ahol feltevésünk szerint

ω_{H}

a Hold szögsebessége:

\begin{matrix} ω_{H}^{2} = \frac{f M}{R^{3}} . \end{matrix}

Ha a műhold tényleg

ω_{H}

szögsebességű pályán kering, akkor mindig a fent számolt konstans erők valamelyikét érzi, hisz az erőtér együtt fordul el vele. Vagyis a keresett pálya tényleg létezik, ha van olyan

ϱ

, amely kielégíti a következő egyenletet:

\begin{matrix} μ ϱ \frac{f M}{R^{3}} = \frac{f M μ}{ϱ^{2}} \pm \frac{f m μ}{{(R \pm ϱ)}^{2}} (- és + sorrend kizárva). \end{matrix}

Rendezve:

\begin{matrix} ϱ = R^{3} (\frac{1}{ϱ^{2}} \pm \frac{m}{M} \cdot \frac{1}{{(R \pm ϱ)}^{2}}) . \end{matrix}

Ebből:

\begin{matrix} R^{3} {(R \pm ϱ)}^{2} \pm \frac{m}{M} ϱ^{2} R^{3} - ϱ^{3} {(R \pm ϱ)}^{2} = 0. \end{matrix}

Ez ötödfokú egyenlet

ϱ

-ra.
Vizsgáljuk meg, hogy van-e az említett esetek valamelyikében pozitív valós

ϱ

értéket adó megoldás.
1. eset:

\begin{matrix} f (ϱ) = R^{3} {(R + ϱ)}^{2} + \frac{m}{M} ϱ^{2} R^{3} - ϱ^{3} {(R + ϱ)}^{2} = 0. \end{matrix}

Tekintsük a bal oldalt

ϱ

polinomjának, és vizsgáljuk az értékét

ϱ = R

és

ϱ = 2 R

helyeken:

\begin{matrix} f (ϱ = R) = + \frac{m}{M} R^{5} > 0, \\ f (ϱ = 2 R) = 9 R^{5} + \frac{m}{M} 4 R^{5} - 72 R^{5} < 13 R^{5} - 72 R^{5} < 0, mivel \frac{m}{M} < 1. \end{matrix}

Vagyis az

f (ϱ)

polinomnak

R

és

2 R

között van zérus helye, hisz az

[R,2 R]

intervallum egyik végén pozitív, a másikon negatív, tehát valahol közben a nullán is átment. Az

f (ϱ)

-t

ϱ

függvényében felrajzolva:

\begin{matrix} ϱ_{1} \approx 1,001 \cdot R . \end{matrix}

2. eset:

\begin{matrix} f (ϱ) & = R^{3} {(R - ϱ)}^{2} - \frac{m}{M} ϱ^{2} R^{3} - ϱ^{3} {(R - ϱ)}^{2}, \\ f (0) & = + R^{5} > 0, \\ f (R) & = - \frac{m}{M} R^{5} < 0. \end{matrix}

Tehát

[0, R]

intervallumon belül van megoldása az egyenletnek. Grafikusan megoldva:

\begin{matrix} ϱ_{2} = 0,85 \cdot R . \end{matrix}

3. eset:

\begin{matrix} f (ϱ) & = R^{3} {(R - ϱ)}^{2} + \frac{m}{M} ϱ^{2} R^{3} - ϱ^{3} {(R - ϱ)}^{2}, \\ f (R) & = + \frac{m}{M} R^{5} > 0, \\ f (2 R) & = R^{5} + \frac{m}{M} 4 R^{5} - 8 R^{5} < - 3 R^{5} < 0. \end{matrix}

R

és

2 R

között itt is van megoldás.
Grafikusan megoldva:

ϱ_{3} \approx 1, 17 \cdot R

.
Tehát létezik a kívánt tulajdonságokkal rendelkező pálya, sőt a megoldásból látszik, hogy legalább

3

ilyen pálya van.

Gnädig Péter (Budapest)

Megjegyzés. Szalay Sándor (Debrecen) megmutatta, hogy ha figyelembe vesszük azt, hogy a Föld is kering a rendszer közös súlypontja körül, akkor a Föld és Hold középpontját összekötő egyenesen kívül is található olyan pont (ún. Lagrange-pont), ahová a műholdat elhelyezve, az keringés közben nem változtatja helyzetét sem a Földhöz, sem a Holdhoz képest.