Feladat: 1989. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balogh József ,  Benczúr Péter ,  Benkő Dávid ,  Bodor András ,  Boncz András ,  Fleiner Tamás ,  Gerlits Ferenc ,  Hausel Tamás ,  Pór Attila ,  Sebestyén Géza ,  Sustik Mátyás ,  Újváry-Menyhárt Zoltán 
Füzet: 1990/február, 51 - 57. oldal  PDF  |  MathML 
Témakör(ök): Kör geometriája, Pitagorasz-tétel alkalmazásai, Síkgeometriai számítások trigonometriával, Szélsőérték differenciálszámítással, Trigonometrikus függvények, Törtfüggvények, Vetítések, Párhuzamos szelők tétele és megfordítása, Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Ellipszis, mint kúpszelet, Középpontos és egyéb hasonlósági transzformációk, Másodfokú (és arra visszavezethető) egyenletek, Pont körre vonatkozó hatványa, Szélsőérték-feladatok differenciálszámítás nélkül, Koordináta-geometria, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1990/február: 1989. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.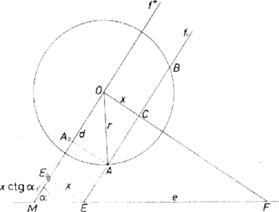

 
 

1. ábra
 

A következő jelöléseket fogjuk használni (lásd az 1. ábrát). A kör középpontja O, sugara r, az O-n át f-fel párhuzamosan húzott egyenes f*, metszéspontja e-vel M, az e és f közti hegyes vagy derékszög α; egy f-fel párhuzamos f1 egyenes metszéspontja e-vel E, a körrel A és B (E,A,B sorrendben); AB felezőpontja C, a CO egyenes metszéspontja e-vel, (ha létezik), F, OC=x, tekintsük pozitívnak, ha C az e és f közti hegyesszögű (illetőleg, ha merőlegesek az egyik) szögtartományban van, negatívnak, ha a másikban; végül OM=d.
 

I. megoldás. A feladatban szereplő szakaszokat kifejezzük a bevezetett mennyiségekkel. AB=2AC=2r2-x2. EA meghatározásához vetítsük E-t és A-t f*-ra, vetületük legyen E0, ill. A0. Ekkor A0A=x, ahol |x|≦r és
EA=E0A0=d-ME0-A0O=d-x ctg α-r2-x2.
A keresett arány tehát
ABAE=2r2-x2d-x ctg α-r2-x2=2d-x ctg αr2-x2-1.
Ez akkor a legnagyobb, ha a nevezőben levő tört a legkisebb értékét veszi fel. Ez a tört pozitív, mert d-x ctg α=E0O=EC és e a körön kívül van, tehát ugyanott veszi fel legkisebb értékét, ahol a négyzete, (d-x ctg α)2/(r2-x2).
Ha x r-hez, vagy -r-hez közeledik, akkor a tört felvesz tetszés szerint nagy értékeket, így legkisebb értékét a számköz belsejében veszi fel, az tehát helyi szélsőérték is, s így ott a tört deriváltja 0. A derivált nevezője pozitív az egész számközben. Számlálója

2(-ctgα)(d-x ctg α)(r2-x2)-(-2x)(d-x ctg α)2==2(d-x ctg α)(dx-r2 ctg α).

Láttuk, hogy az első zárójelben álló mennyiség pozitív, így a derivált a
dx0=r2 ctg α(1)
összefüggésnek eleget tevő helyen tűnik el. Itt negatív értékből megy át pozitívba, tehát a függvénynek itt minimuma van. (Ez egyébként abból is következik, hogy csak egy szélsőérték adódott, egy minimumhelynek viszont kell lennie.)
Többféleképpen is szerkeszthetjük x0-t. Ha x0=0 (azaz α=90∘, e és f merőleges), akkor az O-n át e-re merőlegesen húzott egyenesre a legnagyobb a kérdéses arány (ez egyébként közvetlenül is világos). Ennek szerkesztése közismert.
Ha α hegyes szög, írjuk (1)-et ilyen alakban:
x0r=r ctg αd.(2)

 
 

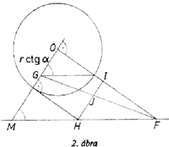Messe az OF-nek a körrel való metszéspontján át e-vel párhuzamosan húzott egyenes f*-ot G-ben (2. ábra). Ekkor GO=r ctg α, (2) jobb oldala tehát a GO/MO aránnyal egyenlő. Ezt akarjuk úgy vetíteni, hogy a nevező r hosszúságú szakaszba menjen át. Messe az MO és a kör metszéspontján át MO-ra merőlegesen állított egyenes e-t H-ban, a H-ból OF-re bocsájtott merőleges utóbbit I-ben, végül FG és HI metszéspontja legyen J. Ekkor HI=r, és így a párhuzamos szelők tétele szerint GO/MO=JI/HI=JI/r. A keresett x0 szakasz tehát JI. Ezt felmérve O-ból OF-re és végpontjában merőlegest állítva OF-re kapjuk a keresett egyenest.
 

Megjegyzések: 1. A szelő jellemzésére használhatjuk pl. az AOC szöget, vagy más paramétert is.
2. A (2) jobb oldalán álló törtet tg α-val bővítve az x0/r=r/d ctg α összefüggést kapjuk. Itt d tg α=OF (3. ábra), így a nyert egyenlőségből leolvasható, hogy az AOC és az FOA háromszög hasonló. Az O-nál levő szögük ugyanis közös és egy megfelelő oldalpárjuk aránya egyenlő. Az előbbi háromszög C-nél levő szöge derékszög, tehát az utóbbiban FA merőleges az OA körsugárra. A keresett szelő metszéspontjai a körrel tehát az F-ből húzott érintők érintési pontjai. Ezt nem nehéz közvetlenül belátni.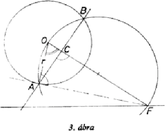
 
 

II. megoldás: Legyen α hegyesszög. Az f-fel párhuzamos érintőkre az AB/EA arány 0, aminél lehet nagyobb is. Akkor a legnagyobb, amikor az AC/EA arány, ez pedig akkor, amikor a reciproka a legkisebb. Azt még 1-gyel növelve az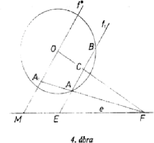
EAAC+1=EA+ACAC=ECAC
arány minimumát szolgáltató szelőt keressük.
 
 

FA és MO metszéspontját A1-gyel jelölve EC/AC=MO/A1O (4. ábra). Itt a számláló nem függ a szelő helyzetétől, így az arány akkor a legkisebb, amikor a nevező a legnagyobb, ez pedig az F-ből húzott érintő érintési pontjára teljesül.
Az F-ből húzott érintők érintési pontját az OF átmérőjű kör metszi ki az adott körből.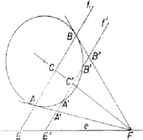
 
 

5. ábra
 

Legyen most f1 ezeken a pontokon átmenő szelő, f' egy másik, és azon E',A',C' a megfelelő metszéspontok, A* pedig az FA-val való metszéspont (5. ábra). Ekkor
E'A'>E'A*,A'C'<A*C',  tehát  A'C'/E'A'<A*C'/E'C',
vagyis a feladatban kérdezett arány valóban a megszerkesztett egyenesen a legnagyobb.
Ha e és f merőleges, akkor f*-ra lesz EB a lehető legnagyobb, EA pedig a legkisebb, tehát a vizsgált arány a legnagyobb. Ennek az egyenesnek a szerkesztése közismert.
 

Megjegyzések. 1. Okoskodhatunk a következő módon is. Tetszés szerinti f1 szelőt véve, a kört egy OF tengelyű és EC/AC arányú merőleges affinitás olyan ellipszisbe viszi át, amelyiknek van közös pontja e-vel. Ha van az ellipszisnek pontja az e-nek a kört nem tartalmazó partján is, akkor az F-ből húzott egyik érintő is ezen az oldalon van, és annak az érintési pontját egy kisebb arányú affinitás viszi át e-re (6. ábr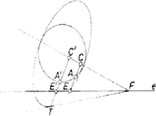a).
 
 

6. ábra
 

Az arány tehát akkor a legkisebb, ha az e-t érintő ellipszist kapjuk, vagyis e az F-ből a körhöz húzott érintő képe. Arra a szelőre lesz tehát a nyújtás aránya a legkisebb, s így a feladatban kérdezett arány a legnagyobb, amelyik az F -ből húzott érintő érintési pontján megy át. Ezen az úton oldotta meg a feladatot Újváry-Menyhárt Zoltán.
2. Gerlits Ferenc számítással oldotta meg a feladatot, de az analízis használata helyett csak a másodfokú egyenletekre vonatkozó ismeretekre támaszkodva.
 

III. megoldás. Az I. megoldásban láttuk, hogy azt az x értéket kell megkeresnünk, amelyikre a (d-x ctg α)2r2-x2=c arány a legkisebb. Más szóval a legkisebb c-t, amelyikre a
(c+ctg2α)x2-(2d ctg α)x+d2-cr2=0
egyenletnek van megoldása, annak abszolút értéke r-nél kisebb és c pozitív. Az egyenletnek akkor van (valós) megoldása, ha nem negatív a diszkriminánsa. A diszkrimináns
4(d2 ctg2α-(c+ctg2α)(d2-cr2))=4c(cr2-(d2-r2ctg2α)).
Ez kell, hogy ne legyen negatív. Mivel c-nek pozitívnak kell lennie, tehát a második tényező sem lehet negatív. Innen
c≧(d2-r2 ctg2α)/r2.
Ha ezt a kritikus értéket beírjuk az egyenletbe, az
((d/r)x-r ctg α)2=0
alakra hozható. Ez az I. megoldásban nyert, r-nél kisebb x0 értéket szolgáltatja.
 

IV. megoldás. Húzzunk A-n át párhuzamost e-vel, messe ez a kört másodszor D-ben. Ha érintőt kapunk, akkor D=A (7.a, b, c áb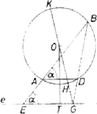ra).
 
 

7.a ábra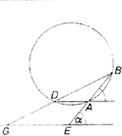
 

 
 

7.b ábra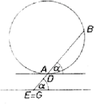
 

 
 

7.c ábra
 

Ekkor a rövidebb BD ívet α szögű (esetleg csúcs-) szögtartomány foglalja magába, így a BD húr hossza csak α-tól függ, az AB szelő helyzetétől nem. BD és e metszéspontját G-vel jelölve a párhuzamos szelők tétele szerint AB/EA=DB/GD. Ez tehát akkor a legnagyobb, ha GD a legkisebb, egyúttal, BD állandó volta miatt GB is, s így GD⋅GB, ami G hatványa a körre, szintén a legkisebb. Ez a szorzat minden G-n átmenő szelőre ugyanakkora, így az O-n átmenőre is. Ennek a körbe eső húrja átmérő, független a G pont helyzetétől, így a hatvány az e egyenesnek a körhöz legközelebb eső pontjára, O-nak e-n való T merőleges vetületére lesz a legkisebb. Az ezt szolgáltató, f-fel párhuzamos egyenest kell tehát megszerkesztenünk.
Az egyenlő hosszúságú húrok egy O középpontú (rcosα sugarú) kör érintői. Ehhez a körhöz megszerkesztjük T-ből a két érintőt. Mindkettőnek a T-től távolabbi metszéspontját a másik közelebbi metszéspontjával kötve össze, két egyenest kapunk (8. ábra), amelyek α nagyságú szöget zárnak be e-vel egyik, illetőleg másik irányban. Egyikük tehát párhuzamos f-fel. A követett gondolatmenet megfordításával látható, hogy ez valóban a keresett egyenes.
Ezt a megoldást Fleiner Tamás adta.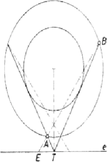
 
 

8. ábra
 

V. megoldás. Ismét deriváltat használunk, de kiszámítása helyett geometriai jelentéséből vonunk le következtetéseket.
Legyen α hegyesszög. Koordinátatengelyeknek válasszuk az O-n átmenő, f-re merőleges és a vele párhuzamos egyenest. Ekkor CA az OC=x változónak azt a -r≦x≦r számközön értelmezett g függvényét szemlélteti, amelyiknek a képe a tengely fölötti félkör, AE pedig ugyanezen a szakaszon azt a h függvényt, amelyre g+h képe az e egyenesnek a szakasz feletti része. A g/h függvény legnagyobb értékét keressük.
Ez a függvény értelmezve van az egész számközön, mivel e-nek nincs közös pontja a körrel, s így a nevező nem 0. A végpontokban a hányados értéke 0, máshol pozitív, így maximuma helyi maximum is, ott a derivált 0, s így annak számlálójára:
g'h-gh'=0(3)
teljesül. Itt g' a kör A-ban húzott érintőjének az iránytangense, h' pedig a (g+h)'=g'+h' összefüggésből kapható. Itt ugyanis a bal oldalon az e egyenes iránytangense, tg α áll, tehát
h'= tg α-g'.
Innen látjuk, hogy a két derivált nem lehet egyszerre 0, tehát (3) csak úgy teljesülhet, ha egyik sem 0.
 
 

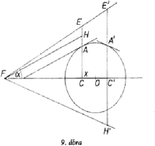9. ábra
 

Húzzunk F-ből párhuzamost az A-ban húzott érintővel (9. ábra), jelöljük CA-val való metszéspontját H-val. Ez a tartomány belsejében levő C pontokra mindig létezik. Ekkor  tg α=CE/FC, az érintő iránytangense CH/FC (negatív, ha H a tengely alatt van), így h'=CE/FC-CH/FC=HE/FC (negatív, ha H az e egyenes fölött van).
Írhatjuk (3)-at, mivel fennállása esetén a deriváltak nem tűnhetnek el, g'h'=g/h alakban. A jobb oldali arány CA/AE-vel egyenlő, a bal oldalon álló pedig megállapításaink szerint a következővel:
CHFCHEFC=CHHE.
Rögzített C és E pontok mellett a CE egyenes különböző P pontjaira a CP/PE arány különböző, ha előjeles arányt nézünk, mint esetünkben. A (3) egyenlőség tehát csak akkor állhat fenn, ha H=A, vagyis az F-en át az A-beli érintővel párhuzamosan húzott egyenes átmegy A-n, azaz A az F-ből a körhöz húzott érintő érintési pontja. Ezzel először is azt kaptuk, hogy a törtnek egy szélsőértéke van, mivel pedig kell egy maximumának lennie, így ez a szélsőérték maximum. Azt is kaptuk, hogy ezt az F-ből a körhöz húzott érintő érintési pontján átmenő egyenes szolgáltatja.
 
Megjegyzés. A bizonyítás szellemes alapötlete Bodor András dolgozatában található. Számos, analízisbeli eszközöket használó megoldással ellentétben a megoldás geometriai tartalmát mutatja meg. Ez természetesen egyszerűbben nyerhető elemi úton, mint pl. a II. megoldásban láttuk.