Kezdőlap


Feladat:	Gy.2796	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csekő Lehel , Gincsai Tibor , Kozma Róbert , Nagy Katalin , Nyakas Péter , Újváry-Menyhárt Mónika
Füzet:	1993/március, 120 - 121. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Szögfelező egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/október: Gy.2796

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szögfelezőtétel szerint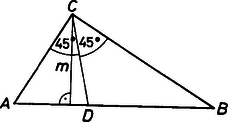

\begin{matrix} A D = \frac{C A}{C A + C B} \cdot A B & (1) \end{matrix}

és

\begin{matrix} D B = \frac{C B}{C A + C B} \cdot A B . \end{matrix}

1. ábra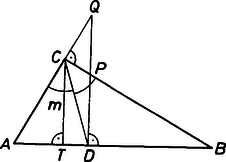

2. ábra

Írjuk fel kétféleképpen az

A B C

háromszög területét:

\begin{matrix} T_{A B C} = \frac{A B \cdot m}{2} = \frac{C A \cdot C B}{2}, \end{matrix}

tehát

\begin{matrix} m = \frac{C A \cdot C B}{A B} . & (2) \end{matrix}

Először megmutatjuk, hogy

A D < m

. (1) és (2) szerint

\begin{matrix} A D < m \Leftrightarrow \frac{C A \cdot B A}{C A + C B} < \frac{C A \cdot C B}{A B}, \end{matrix}

azaz

\begin{matrix} A B^{2} - C B^{2} < C A \cdot C B, \end{matrix}

ez pedig Pitagorasz tétele

(A B^{2} = C A^{2} + C B^{2})

miatt ekvivalens a

C A^{2} < C A \cdot C B

, vagyis a

C A < C B

egyenlőtlenséggel.
Ugyanúgy láthatjuk be azt is, hogy

m < D B

II. megoldás. Jelöljük a háromszög

C

-ből induló magasságának talppontját

T

-vel. Mivel

C B > C A

, ezért

C A B ∢ > C B A ∢

. Nyilvánvaló, hogy

B C T ∢ = C A B ∢

és

A C T ∢ = C B A ∢

, ezért

B C T ∢ > A C T ∢,

tehát

A D > A T

. A

D

pontban az

A B

átfogóra állított merőleges a

B C

és

A C

oldalegyeneseket a

P

és

Q

pontokban metszi az ábrának megfelelően.
A szögfelezőtétel szerint

\frac{B D}{A D} = \frac{B C}{C A} .

A B C

háromszög hasonló a

P B D

és az

A Q D

háromszögekhez, hiszen szögeik megegyeznek; tehát

\begin{matrix} \frac{D B}{A D} = \frac{B C}{C A} = \frac{D B}{D P} = \frac{D Q}{A D} . \end{matrix}

Innen

A D = D P

és

D B = D Q

adódik.
Figyelembe véve, hogy

D P < m < D Q

, kapjuk, hogy

A D < m < D B

, és ezt kellett bizonyítanunk.

Gincsai Tibor (Nyíregyháza 1.sz. Benczur Gyula Ált. Isk. 8. o. t.)
dolgozata alapján