Kezdőlap


Feladat:	Gy.2123	Korcsoport: 14-15	Nehézségi fok: könnyű
Füzet:	1983/december, 210 - 211. oldal		PDF \| MathML
Témakör(ök):	Húrsokszögek, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/április: Gy.2123

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rajzoljuk meg a $H$ húrsokszög körülírt körét. Két esetet különböztethetünk meg aszerint, hogy $H$ tartalmazza-e a körülírt kör $O$ középpontját vagy sem. Először legyen $O$ a $H$ belsejében vagy határán. Kössük össze $O$ -t a sokszög valamennyi csúcsával! Mivel $H$ konvex és $O$ belső pont, a keletkezett egyenlő szárú háromszögek $H$ -ban vannak. Láthatjuk, hogy az egyenlő szárú háromszögek egyenlő szögei közül az egyik egy páratlan, a másik a szomszédos páros indexű csúcshoz tartozik. Mivel a sokszögnek páros sok csúcsa van, azért a páratlan sorszámú csúcsokban ugyanazokat a szögeket kell összegeznünk, mint a párosokban. Így összegük valóban egyenlő.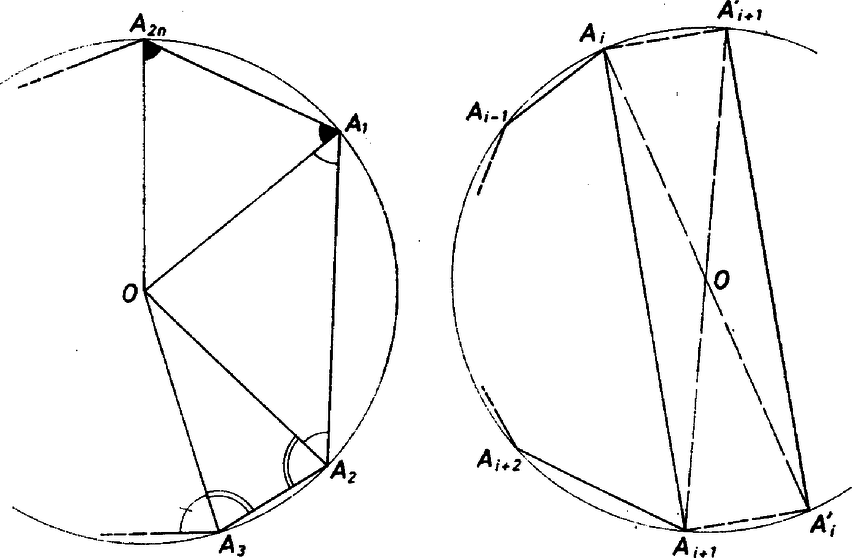

A második esetben

H

nem tartalmazza a körülírt kör

O

középpontját. Ekkor van a sokszögnek olyan

A_{i}, A_{i + 1}

oldala, mely úgy osztja ketté a kört, hogy az egyik részben van a

H,

a másikban az

O

. Tükrözzük az

A_{i} A_{i + 1}

oldalt

O

-ra, a kapott szakasz legyen

A'_{i} A'_{i + 1}

H' = A_{1} A_{2} ... A_{i} A'_{i + 1} A'_{i} A_{i + 1} ... A_{2 n}

húrsokszögnek páros sok oldala van és

O

-t belsejében tartalmazza. Így az előzők szerint a páros sorszámú csúcsaiban levő belső szögeinek

S

összege egyenlő a páratlan sorszámú csúcsban levő belső szögeinek összegével.
Most ha az

S

összegből levonjuk az

A_{i} A_{i + 1} A'_{i}

és

A_{i} A'_{i + 1} A_{i}

szögeket, akkor éppen

H

-nak az

(i + 1)

-gyel egyenlő párosságú csúcsainál található belső szögei összegét kapjuk. Hasonlóan,

S

-ből az

A_{i + 1} A_{i} A'_{i + 1}

és

A'_{i + 1} A_{i} A_{i + 1}

szögeket levonva az

i

-vel egyenlő párosságú csúcsok belső szögeinek összege adódik. Az

A, A_{i + 1} A'_{i} A'_{i + 1}

idom téglalap, tehát

S

-ből mindkét esetben ugyanannyit,

90^{\circ} + 90^{\circ} = 180^{\circ}

-ot vontunk le. Ez pedig azt mutatja, hogy a

H

-ra vonatkozó megfelelő összegek egyenlők, állításunkat erre az esetre is bizonyítottuk.