Kezdőlap


Feladat:	Gy.2043	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1983/április, 154 - 155. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1982/március: Gy.2043

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a téglalap hosszabbik oldalát $a$ -val. Az $A, B$ pontokon átmenő kör középpontja $O_{1}$ rajta van az $A B$ szakasz felező merőlegesén, messe ez $A B$ -t $F_{1}$ -ben. Hasonlóan az $A D$ szakasz felező merőlegese messe 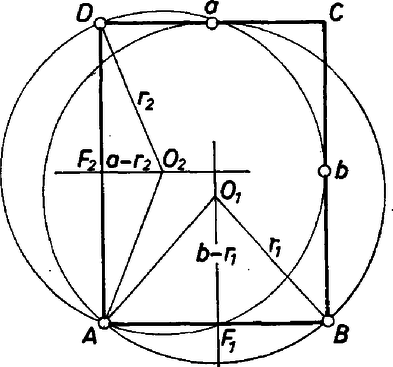$A D$ -t $F_{2}$ -ben.

O_{1} F_{1} B

, ill.

O_{2} F_{2} A

derékszögű háromszögre felírhatjuk Pitagorasz tételét:

\begin{matrix} r_{1}^{2} = {(\frac{a}{2})}^{2} + {(| b - r_{1} |)}^{2} \\ r_{2}^{2} = {(\frac{b}{2})}^{2} + {(| a - r_{2} |)}^{2} . \end{matrix}

O_{1} F_{1} = b - r_{1}

, ill.

r_{1} - b

aszerint, hogy a kör középpontja a téglalap belsejébe esik vagy sem. A négyzetre emelés után mindkettő ugyanazt az eredményt adja, azaz

\begin{matrix} r_{1} = \frac{a^{2} + 4 b^{2}}{8 b} és r_{2} = \frac{b^{2} + 4 a^{2}}{8 a} . \end{matrix}

Ezt (1)-be helyettesítve kapjuk, hogy

\begin{matrix} a (a^{2} + 4 b^{2}) + b (b^{2} + 4 a^{2}) ≧ 5 a b (a + b) . \end{matrix}

Ennek az egyenlőtlenségnek a helyességét kell igazolnunk.
Rendezés után

\begin{matrix} a^{3} - a^{2} b - a b^{2} + b^{3} ≧ 0. \end{matrix}

Tovább alakítva kapjuk, hogy

\begin{matrix} a^{2} (a - b) - b^{2} (a - b) = (a^{2} - b^{2}) (a - b) = {(a - b)}^{2} (a + b) \end{matrix}

s ez valóban nagyobb vagy egyenlő

0

, hiszen

a

és

b > 0

. Egyenlőség csak akkor állhat fenn, ha

a = b

, azaz az idom négyzet.