Kezdőlap


Feladat:	F.2468	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alexy M. , Argay Gy. , Badics T. , Bán Rita , Bujdosó L. , Csermely Ágnes , Fortenbacher T. , Fülöp T. , Hajdú S. Z. , Hegedűs P. , Hraskó A. , Íjjas Cs. , Ispány Márton , Kaiser A. , Karácsony P. , Kerner Anna , Kisdi B. , Komorowitz J. , Kopanecz G. , Kós G. , Kovács 111 S. , Kruzslicz F. , Ladányi L. , Limbek Cs. , Magyar Á. , Megyesi G. , Michelcsik Éva , Németh Buhin Á. , Olasz Szabó M. , Paál Beatrix , Pfeil T. , Pintér A. , Prokaj V. , Ribényi Á. , Sárközy G. , Simon Gy. , Simon P. , Somogyi Á. , Szabó Szabolcs , Szalay Gy. , Szente A. , Uhlmann E. , Varga K. , Varga L.
Füzet:	1985/március, 104 - 106. oldal		PDF \| MathML
Témakör(ök):	Permutációk, Egységgyökök, Komplex számok, Polinomok szorzattá alakítása, Racionális együtthatós polinomok, Egyéb sokszögek geometriája, Vektorok lineáris kombinációi, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1984/március: F.2468

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ilyen $n$ -szög létezésének szükséges és elégséges feltétele, hogy az $1$ , $2$ , $3$ , $...$ , $n$ hosszúságú, megfelelő irányú vektorok összege a nullvektor legyen. Megfelelő irányon azt értjük, hogy bármely két egymás utáni oldalvektor iránykülönbsége a forgási irányt is beleértve $360^{\circ} / n,$ ti. amennyi az egyenlő szögű konvex $n$ -szög külső szöge. Jelöljük $i = 1$ , $2$ , $...$ , $n$ -re az $i$ -edik oldal hosszát $a_{i}$ -vel, az oldallal egyező irányú egységvektort $x_{i}$ -vel. Az $x_{i}$ vektorokat közös kezdőpontból felmérve azok végpontjai szabályos $n$ -szöget határoznak meg.
Feladatunk tehát az $1$ , $2$ , $...$ , $n$ számoknak olyan $a_{1}$ , $...$ , $a_{n}$ permutációját meghatározni, amire az

\begin{matrix} a_{1} x_{1} + a_{2} x_{2} + ... + a_{n} x_{n} \end{matrix}

(1)

vektorösszeg éppen a nullvektor. Ha sikerül ilyen permutációt találnunk, akkor az

a_{1} x_{1}

a_{2} x_{2}

stb. vektorokat egymás után fölmérve, egy záródó konvex

n

-szöget kapunk, amelynek szögei egyenlők, oldalai pedig valamilyen sorrendben

1

2

3

...

n

hosszúságúak. Ha pedig nincs ilyen permutáció, akkor a megfelelő sokszög sem létezik.

1. ábra

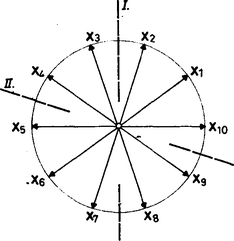Térjünk most rá az

n = 10

esetre. A közös kezdőpontból induló

x_{1}

...

x_{10}

vektorokat az 1. ábra mutatja. Az (1) vektorösszeg pontosan akkor 0, ha két, nem párhuzamos egyenesre eső vetülete is 0. Az egyik egyenes legyen az

x_{10}

(és

x_{5}

) vektorokra merőleges egyenes. Az

a_{i} x_{i}

ilyen irányú komponense

a_{i} sin (i \cdot 36^{\circ}

). A

sin i \cdot 36^{\circ}

tényező abszolút értéke ‐ azon fölül, hogy

i = 5

és

i = 10

esetén 0 ‐ kétféle értéket vehet föl az összegezés során. Ennek alapján a tagokat két zárójelbe gyűjtjük:

\begin{matrix} (a_{1} + a_{4} - a_{6} - a_{9}) sin 36^{\circ} + (a_{2} + a_{3} - a_{7} - a_{8}) sin 72^{\circ} = 0. & (1) \end{matrix}

Feladatunkban a zárójelek értéke egész szám, másrészt

\begin{matrix} \frac{sin 72^{\circ}}{sin 36^{\circ}} = 2 cos 36^{\circ} = \frac{\sqrt[]{5} + 1}{2} \end{matrix}

irracionális szám. Emiatt az egyenlőség csak úgy teljesülhet, ha a zárójelek értéke külön-külön 0. Ezt mindjárt így írjuk:

\begin{matrix} a_{1} - a_{6} = a_{9} - a_{4} & (2) \\ a_{3} - a_{8} = a_{7} - a_{2}, & (3) \end{matrix}

továbbá (2) és (3) teljesülése esetén az (1) összegvektor

x_{10}

-re merőleges vetülete 0.
Megismételve az eljárást az

x_{2}

és

x_{7}

vektorokra merőleges egyenesre is, adódik, hogy (1)-nek erre eső vetülete akkor és csak akkor, 0, ha

\begin{matrix} a_{3} - a_{8} = a_{1} - a_{6} \end{matrix}

(4)

valamint

\begin{matrix} a_{5} - a_{10} = a_{9} - a_{4} \end{matrix}

(5)

egyaránt fennáll.
Észrevesszük, hogy (2) két oldalának közös értékét

d

-vel jelölve (2)‐(5) éppen azt mondja ki, hogy a keresett tízszög szemközti, párhuzamos oldalpárjai hosszának különbsége ‐ alkalmas irányban véve ‐ egyenlő. És úgy lesznek előjelre nézve is egyenlők, ha pl. mindig a páratlan indexű oldalból vonjuk ki a szemben fekvő, tehát páros indexű oldal hosszát. S mivel ilyen esetben (2)‐(5) automatikusan teljesül is, a tízszög záródni fog.
Már ennyi elég ahhoz, hogy példát adhassunk a kívánt tízszögre.

d = - 5

esetén az (

a_{i}, a_{i + 5}

) szemben fekvő oldalpár számára

i = 1

2

3

4

5

mellett vehető a következő oldalhossz-párok tetszőleges permutációja:

\begin{matrix} \frac{a_{i} 1 7 3 9 5}{a_{i + 5} 6 2 8 4 10} \end{matrix}

Másik példa az oldalhosszak párba állítására

d = - 1 :

\begin{matrix} \frac{a_{i} 1 4 5 8 9}{a_{i + 5} 2 3 6 7 10} \end{matrix}

Befejezésül belátjuk, hogy

| d |

az előírt oldalhosszak mellett csak 1 vagy 5 lehet. Jelöljük a páratlan indexű oldalak összegét

U

-val, a párosakét

P

-vel, ekkor a föntiek szerint

U - P = 5 d

, másrészt

U + P = 55

, amiből

\begin{matrix} \frac{U}{5} = \frac{11 + d}{2}, \frac{P}{5} = \frac{11 - d}{2} . \end{matrix}

Eszerint

d

nem lehet páros.
Nyilván nem lehet

d \geq 9

. De még a

d = 7

különbséget is csak három oldalhossz párból lehet előállítani:

\begin{matrix} 7 = 10 - 3 = 9 - 2 = 8 - 1. \end{matrix}

Ha pedig

d = 3

-at követelünk meg, az 5 (és 6) számtól föl- és lefelé 1‐1 szám van 3 egységnyi távolságban: a 2 és a 8, és egyik sem alkothat 3 értékű különbséget máshogy, mint az 5-össel.