Kezdőlap


Feladat:	F.2433	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alexy N. , Argay Gy. , Bán Rita , Bujdosó 419 L. , Cynolter B. , Cynolter G. , Dobos Borbála , Fülöp T. , Giba P. , Hraskó A. , Ilosvay F. , Ispány Márton , Karácsony P. , Kovács 111 S. , Ladányi L. , Limbek Cs. , Mócsy M. , Németh-Buhin Á. , Paál Beatrix , Pintér A. , Prokaj V. , Sáhi A. , Selyem I. , Simon P. , Szabó 112 T. , Szabó 741 Z. , Szabó Sz. , Szakállas Gy. , Szalay Gy. , Szeier T. , Varga 610 J.
Füzet:	1984/január, 14 - 16. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Térfogat, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1983/szeptember: F.2433

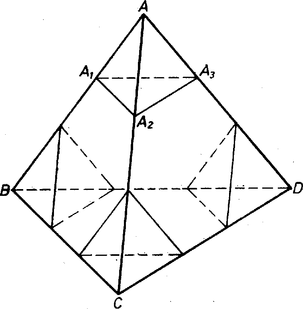
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C D$ tetraéder éleinek hosszát $a$ -val. A tetraéder térfogata $V_{1} = \frac{a^{3} \sqrt[]{2}}{12}$ , felszíne $F_{1} = a^{2} \sqrt[]{3}$ , ezért

\begin{matrix} κ_{1} = \frac{V_{1}^{2}}{F_{1}^{3}} = \frac{\sqrt[]{3}}{648} . \end{matrix}

A B C D

tetraéderből levágandó tetraéderek szintén szabályosak, hiszen minden lapjuk egyenlő oldalú háromszög; az oldalak hossza

λ a

. A poliéderek térfogata minden levágáskor

\frac{a^{3} \sqrt[]{2}}{12} \cdot λ^{3}

-nel csökken, vagyis

\begin{matrix} V_{n} = V [1 - (n - 1) λ^{3}] (n = 2, 3, 4, 5) . \end{matrix}

( Mivel

λ ≦ \frac{1}{2}

, a levágandó tetraéderek nem nyúlnak egymásba, legfeljebb páronként egy közös csúcsuk lehet.)

A poliéder felületéből minden levágáskor három

a λ

oldalú szabályos háromszöget kell eltávolítanunk, majd egy ugyanilyen háromszöget hozzá kell raknunk, mivel a levágott tetraédernek egyik lapja a csonkítandó test belsejében volt, levágás után viszont ez a lap is része az új test felületének. A poliéderek felszíne tehát minden levágáskor

\frac{a^{2} \sqrt[]{3}}{2} \cdot λ^{2}

-nel csökken, ezért

\begin{matrix} F_{n} = F_{1} [1 - (n - 1) \frac{λ^{2}}{2}] (n = 2, 3, 4, 5.) \end{matrix}

Ezek szerint a

κ

számok további értékei:

\begin{matrix} κ_{n} = \frac{{(1 - (n - 1) λ^{3})}^{2}}{{(1 - (n - 1) \frac{λ^{2}}{2})}^{3}} \cdot κ_{1} \end{matrix}

(

n = 2, 3, 4, 5

, a képlet

n = 1

-re is igaz.)
Belátjuk, hogy rögzített

0 < λ ≦ \frac{1}{2}

érték mellett

n

növekedtével

κ_{n}

nő.
Segítségül vesszük folytonosan változó

x

esetére az

\begin{matrix} f (x) = \frac{{(1 - λ^{3} x)}^{2}}{{(1 - \frac{λ^{2}}{2} x)}^{3}} \end{matrix}

függvényt, amely az

x = 0

1

2

3

4

egész értékek mellett rendre a

κ_{1}

κ_{2}

κ_{3}

κ_{4}

κ_{5}

értéket veszi fel és

f (0) = 1

. Belátjuk, hogy

f (x)

0 ≦ x ≦ 4

intervallumban szigorúan monoton növekvő, ugyanis deriváltja állandóan pozitív. (A nevező az

x = \frac{2}{λ^{2}}

helyen válik zérussá, ez azonban kívül esik a vizsgálni kívánt intervallumon, mivel

2 / λ^{2} ≧ 8

; mindjárt említjük a számláló zérushelyét is:

x = 1 / λ^{3} ≧ 8

.) Ezekből következik, hogy a kiragadott egész

x

-ek mellett is teljesül:

\begin{matrix} κ_{1} < κ_{2} < κ_{3} < κ_{4} < κ_{5} . \end{matrix}

Áttérünk a szokásos jelölésekre, legyen

\begin{matrix} u (x) = {(1 - λ^{3} x)}^{2}, v (x) = {(1 - \frac{λ^{2}}{2} x)}^{3} . \end{matrix}

Az ismert deriválási szabályok szerint

\begin{matrix} f' (x) = (\frac{u (x)}{v (x)})' = \frac{u' (x) \cdot v (x) - u (x) \cdot v' (x)}{v^{2} (x)} = \\ = \frac{1}{{(1 - \frac{λ^{2}}{2} x)}^{6}} (- 2 λ^{3} (1 - λ^{3} x) {(1 - \frac{λ^{2}}{2} x)}^{3} + \frac{3}{2} λ^{2} {(1 - λ^{3} x)}^{2} {(1 - \frac{λ^{2}}{2} x)}^{2}) = \\ = \frac{λ^{2}}{2} \cdot \frac{1 - λ^{3} x}{{(1 - \frac{λ^{2}}{2} x)}^{4}} (- 4 λ (1 - \frac{λ^{2}}{2} x) + 3 (1 - λ^{3} x)), \end{matrix}

és itt mind a három tényező pozitív a

[0; 4]

intervallumban; a nagy zárójel:

\begin{matrix} 3 - 4 λ - λ^{3} x ≧ 1 - \frac{x}{8} > 0. \end{matrix}

Evvel bebizonyítottuk állításunkat.
Az is belátható, hogy rögzített

n

esetén

κ_{n}

értéke növekszik, ha

λ

értéké a megadott határokon belül nő, a feladat kérdése azonban nem erre vonatkozott.

Megjegyzés. Emlékeztetjük az olvasót a konvex síkidomok izoperimetrikus hányadosára,

t / p^{2}

-re (F. 2395. feladat, KöMaL 1983. szept. szám, 11. oldal). Itt a konvex testek ugyanilyenféle jellemző számáról van szó. Ott

t^{1}

és

p^{2}

kitevője ‐ fölcserélve ‐ abból adódik, hogy a terület

2

dimenziós méret, a kerület (hosszúság)

1

dimenziós. Itt pedig

F

és

V

dimenziószáma

2

, ill.

3

. Ezekből

t / p^{2}

és

V^{2} / F^{3}

dimenziója egyaránt

0

, ami azt jelenti, hogy a hányados nem függ az egységek megválasztásától, ha

V

és

F

egységét ugyanabból a hosszegységből származtatjuk.
Konvex síkidomokra

t / p^{2}

legnagyobb értéke

1 / 4 π

, a körre; a konvex testeknél pedig

κ

a gömbre a legnagyobb:

1 / 36 π

. Ez az ún. izoperimetrikus probléma. (Kockára

1 / 216

, négyzetre

t / p^{2} = 1 / 16

. )
Eredményünket szemléletesen így fejezhetjük ki: az egymás után

1

2

3

4

tetraéder levágásával kapott testek lépésről lépésre haladnak a ,,gömbszerűség'' felé.

λ = 1 / 2

esetén a negyedik levágás eredménye szabályos oktaéder.