Kezdőlap


Feladat:	F.2427	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bán Rita , Birkás Gy. , Böröczky L. , Csillag P. , Danyi P. , Erdős L. , Hetyei G. , Hraskó A. , Kerner Anna , Megyesi G. , Pelles Tamás , Sáhi A. , Scharle A. , Szabó T. , Szirmai J. , Szöllősi Gabriella , Törőcsik J. , Vindics I.
Füzet:	1983/december, 204 - 205. oldal		PDF \| MathML
Témakör(ök):	Háromszög alapú hasábok, Súlypont, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1983/május: F.2427

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. A feladat szövege szerint az indexezett pontok az $A B C$ síknak az egyik oldalán vannak. Általában azzal a föltevéssel kell kezdenünk a bizonyítást, hogy a $6$ pont különböző.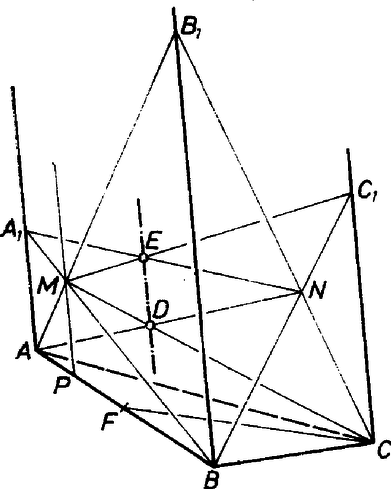

Jelöljük

M

-mel az

A B B_{1} A_{1}

trapéz átlóinak metszéspontját, ez az

A A_{1}

és

B B_{1}

oldalélek közötti pont. Ekkor

D

‐ mint a

C A B_{1}

és

C B A_{1}

síkok közös pontja ‐ rajta van az

M C

egyenesen (a hasáb belsejében), továbbá

E

‐ mint a

C_{1} A B_{1}

és

C_{1} B A_{1}

síkok közös pontja ‐ rajta van az

M C_{1}

egyenesen. Ennélfogva

D

is,

E

is benne van az

M C C_{1}

síkban. Ezt a megállapítást ebben az alakban fogjuk felhasználni:

E

benne van a

D C C_{1}

síkban.
Írjunk a fönti meggondolásban minden

A

betű helyére

B

-t és minden

B, C

helyére

C

-t, ill.

A

-t,

M

helyére

N

-et, de hagyjuk a helyükön az indexeket. Így azt kapjuk, hogy

E

D A A_{1}

síkban is benne van.
Az egymástól különböző

D C C_{1}

és

D A A_{1}

síkok tartalmazzák a

C C_{1},

ill.

A A_{1}

egymással párhuzamos egyeneseket (oldaléleket), ezért metszésvonaluk, a

D E

egyenes párhuzamos az oldalélekkel. Ezt kellett bizonyítanunk.
2. A

D E

egyenes általában nem megy át a kérdésbeli súlypontokon. Messe az

M

-en átmenő,

A A_{1}

-gyel párhuzamos egyenes

A B

-t

P

-ben, legyen másrészt

A B

felezőpontja

F

. Ha

P

és

F

különböző pontok, akkor

F

nincs benne az

M C C_{1} = P C C_{1}

síkban, tehát nincs benne az

A B C

háromszög súlypontja sem. A

D E

egyenesnek nincs pontja az

M C C_{1}

síkon kívül, és így nem mehet át a súlyponton.

P

nyilván akkor és csak akkor esik egybe

F

-fel, ha

A A_{1} = B B_{1} .

Igenlő válaszhoz szükséges a

P

és

F

egyezése, de nem elegendő, hasonló föltételnek kell teljesülnie a további két oldallapon is. Ha

A A_{1} = B B_{1} = C C_{1},

akkor a

D E

egyenes átmegy a hasáb mindkét véglapjának súlypontján.
3. Ha valamelyik oldalél két kijelölt pontja egybeesik, akkor a

D E

egyenes máris határozatlan, egybeesik

D

és

E .

Ha pedig két oldalélen is egybeesik az indexezett pont az indextelennel, akkor vizsgálatunk tárgytalan,

D

és

E

nincsenek meghatározva.

Pelles Tamás (Győr, Czuczor G. Bencés Gimn., III. o. t.)