Kezdőlap


Feladat:	F.2397	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alexy N. , Antall P. , Badics T. , Bán Rita , Bánhegyi B. , Buzás M. , Böröczky L. , Danyi P. , Donkó z. , Drobni A. , Erdős 228 L. , Fáth G. , Fóris Z. , Gulyás Éva , Hegedűs Andrea , Herendi T. , Hetyei G. , Horváth 290 P. , Horváth A. , Hraskó A. , Ilosvay F. , Kántor Cs. , Katona Gy. , Kerner Anna , Kós G. , Kovács 111 S. , Ladányi L. , Márkus A. , Megyesi G. , Mócsy M. , Nyikes P. , Parajdi I. , Pásztor L. , Petrovics Gyöngyi , Rátkay G. , Réz A. , Simon P. , Szabó Cs. , Szirmai J. , Szöllősi Gabriella , Tóth G. , Törőcsik J. , Varga K. , Vindics I. , Virányi L. , Zsigri G.
Füzet:	1983/május, 208. oldal		PDF \| MathML
Témakör(ök):	Térgeometriai bizonyítások, Gömb és részei, Feladat
Hivatkozás(ok):	Feladatok: 1982/december: F.2397

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $G$ középpontját $O$ -val, a $k$ -ra illeszkedő $G_{1}$ és $G_{2}$ gömbök középpontját $O_{1}$ , ill. $O_{2}$ -vel. Tekintsük a három középpont által meghatározott $S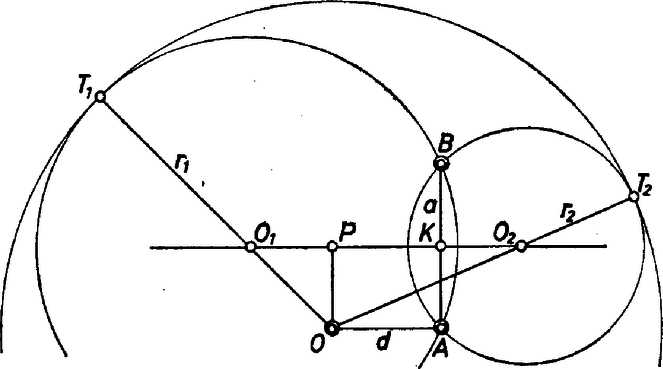$ síkot.

G_{1}

és

G_{2}

centrálisa átmegy

k

-nak

K

középpontján és merőleges

k

síkjára, vagyis

K

is benne van

S

-ben,

k

síkja merőleges

S

-re,

k

-nak

S

-re való vetülete egy

A B

szakasz, melynek hossza egyenlő az átmérővel, és

K

felezi

A B

-t. Továbbá

O

-val együtt

S

-ben van

O

-nak

k

-n levő vetülete, tehát a vetület

A

és

B

egyike, legyen ez mondjuk

A

. (Az

A B

szakasz aszimmetrikus helyzete miatt

S

mindig egyértelműen meg van határozva.)
Síkunk mind a három gömbből főkört metsz ki. A belső gömbök főkörei átmennek az

A, B

pontokon, másrészt érintik a

G

-ből kimetszett főkört, hiszen a gömbök

T_{1}, T_{2}

érintkezési pontjai nyilván rajta vannak az

O O_{1}

, ill.

O O_{2}

centrálison. Így az alakzatból elég vizsgálnunk az

S

-beli metszetet: adva van az

O

középpontú,

R

sugarú

k^{*}

kör és a belsejében egy

A B

szakasz úgy, hogy az

O A B ∢

derékszög; arról a két körről van szó, amelyek átmennek

A

-n és

B

-n, továbbá érintik

k^{*}

-ot. Azt kell belátnunk, hogy az érintő körök sugarainak összege

R

.
Legyen az

O_{i}

középpontú érintő gömb sugara

r_{i}

‐ tehát a főköré is ‐,

A B = 2 a (< 2 R), A O = d (< R)

és

O

vetülete

O_{1} O_{2}

-n

P

, tehát

O P K A

derékszögű négyszög.
Az

O_{i} K A

derékszögű háromszögekből

(i = 1, 2) O_{i} K = \sqrt[]{r_{i}^{2} + a^{2}}

, és igy a

K, O_{i}, P

pontok minden helyzetében

O_{i} P = | O_{i} K \pm d |

valamelyik előjellel, tehát az

O O_{i} P

háromszögből Pitagorasz tételével

\begin{matrix} {(\sqrt[]{r_{i}^{2} + a^{2}} \pm d)}^{2} + a^{2} = {(R - r_{i})}^{2}, (i = 1, 2) \end{matrix}

azaz

\begin{matrix} \pm 2 d \sqrt[]{r_{i}^{2} + a^{2}} = R 2 - 2 R t_{i} - d^{2} . \end{matrix}

Ebből négyzetre emeléssel másodfokú egyenletet kapunk

r_{i}

-re:

\begin{matrix} 4 (R^{2} - d^{2}) r_{i}^{2} - 4 R (R^{2} - d^{2}) r_{i} + {(R^{2} - d^{2})}^{2} + 4 a^{2} d^{2} = 0, \end{matrix}

és ez egyaránt érvényes

r_{1}

-re,

r_{2}

-re. Más gyöke tehát nem lehet, ennélfogva gyökeinek összegére

r_{i}

, és

r_{i}^{2}

együtthatói hányadosának (‐1)-szereséből

\begin{matrix} r_{1} + r_{2} = R, \end{matrix}

ezt kellett bizonyítanunk.