| Feladat: | F.2358 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Ákosfai Z. , Almássy T. , Ambrosz O. , Bán Éva , Böröczky K. , Csörgő T. , Danyi P. , Erdős L. , Fóris Z. , Hetyei G. , Holbok I. , Kovács 123 L. , Lengyel Zs. , Megyesi G. , Mikó Teréz , Mohay T. , Nádor P. , Nagy 548 R. , Pintér G. , Regős Enikő , Reviczky Z. , Szabó 555 L. , Szalai J. , Szemők Á. , Szöllősi Gabriella , Tóth 360 G. , Tranta Beáta , Törőcsik J. , Weisz Ferenc , Zieger B. , Zubor Z. | ||
| Füzet: | 1982/november, 124 - 125. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Szélsőérték-feladatok differenciálszámítás nélkül, Vektorok skaláris szorzata, Szögfüggvények, síkgeometriai számítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1982/március: F.2358 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az általánosság megszorítása nélkül feltehetjük, hogy , s így . 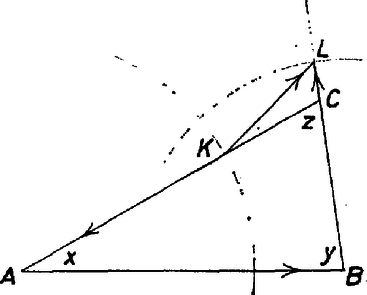 1. ábra Vegyük fel az félegyenesen a pontot úgy, hogy , s a félegyenesen az pontot úgy, hogy legyen. Világos, hogy az középpontú, sugarú körön, pedig a középpontú, sugarú körön van. Elsőként a távolságot határozzuk meg. Ehhez vegyük észre, hogy a vektor a , , vektorok összege, ahonnan
Így a kérdéses kifejezés a maximumát akkor veszi fel, amikor a távolság a minimumát. Ha most a fenti két kör metszi egymást, azaz
Weisz Ferenc (Mohács, Kisfaludy K. Gimn., IV. o. t.) Megjegyzés. Az (1) összefüggést vektorokra való hivatkozás nélkül is megkaphatjuk. Legyen az a pont, amelyre paralelogramma. 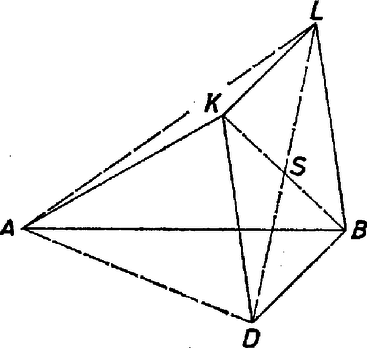 2. ábra Ekkor, a cosinustétel alapján (2. ábra)
|