Kezdőlap


Feladat:	F.2343	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ákosfai Z. , Alberti G. , Almássy T. , Beke S. , Böröczky K. , Csörgő T. , Hetyei G. , Holbok I. , Károlyi Gyula , Magyar Á. , Mikó Teréz , Mohai T. , Nagy 548 R. , Raffai Zs. , Simák Gy. , Szállási Z. , Tranta Beáta , Törőcsik J. , Virányi L. , Zieger B.
Füzet:	1982/szeptember, 13 - 16. oldal		PDF \| MathML
Témakör(ök):	Csonkakúp, Terület, felszín, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1981/december: F.2343

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltehetjük, hogy $R > r$ . Jelöljük a körök külső hasonlósági pontját $H$ -val, a nagyobb kör középpontját $O$ -val, a kisebbét $O'$ -vel, a szelő és az $O H$ egyenes hajlásszögét $α$ -val (1 ábr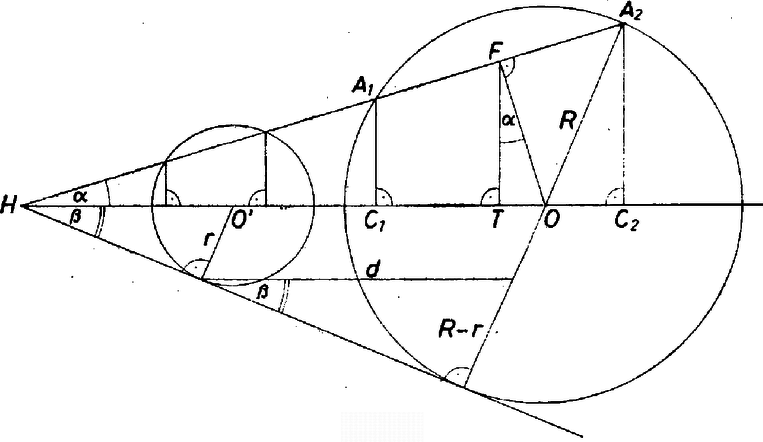a).

1. ábra

A szóban forgó két csonkakúp-palást hasonló (

H

középpontú nyújtással egymásba átvihetők), az egymásnak megfelelő lineáris méretek aránya megegyezik a körök sugarainak arányával, felszíneik aránya pedig e sugarak négyzeteinek arányával. Ha a nagyobb csonkakúp-palást felszíne

P

, akkor a kisebbé

\frac{r^{2}}{R^{2}} P

, különbségük pedig

\frac{R^{2} - r^{2}}{R^{2}} P

. Látható, hogy ez akkor a legnagyobb, amikor

P

maga is a lehető legnagyobb.

(\frac{R^{2} - r^{2}}{R^{2}} > 0, állandó)

.
Fejezzük ki

P

-t

α

függvényeként. Legyenek a szelőnek az

R

sugarú körrel alkotott metszéspontjai

A_{1}

A_{2},

ezekből az

O H

egyenesre bocsátott merőlegesek talppontjai

C_{1}

C_{2}

. A csonkakúp-palást felszínének ismert képlete szerint

\begin{matrix} P = π (A_{1} C_{1} + A_{2} C_{2}) A_{1} A_{2} . \end{matrix}

Legyen még az

O

-ból a szelőre bocsátott merőleges talppontja (egyben az

A_{1} A_{2}

húr felezőpontja)

F

F

-ből az

O H

egyenesre bocsátott merőleges talppontja pedig

T

F T

A_{1} C_{1} C_{2} A_{2}

derékszögű trapéz középvonala, így

\begin{matrix} A_{1} C_{1} + A_{2} C_{2} = 2 F T . \end{matrix}

O F T ∢ = α

, mivel merőleges szárú szögek, és mindkettő hegyesszög. Az

O F T

derékszögű háromszögben tehát

\begin{matrix} F T = O F \cdot cos α . \end{matrix}

Másrészt az

O H F

derékszögű háromszögben

\begin{matrix} O F = O H \cdot sin α, \end{matrix}

továbbá a körök hasonlósága alapján

\begin{matrix} \frac{O H - d}{O H} = \frac{r}{R}; \end{matrix}

ahonnan

\begin{matrix} O H = \frac{d R}{R - r} . \end{matrix}

Ezek szerint

\begin{matrix} F T = \frac{d R}{R - r} sin α cos α . \end{matrix}

O A_{2} F

derékszögű háromszögben

\begin{matrix} A_{2} F = \sqrt[]{R^{2} - O F^{2}} = \sqrt[]{R^{2} - \frac{d^{2} R^{2}}{{(R - r)}^{2}} sin^{2} α} . \end{matrix}

A_{1} A_{2}

húr ennek kétszerese.
A kapott összefüggések alapján a palástfelszín:

\begin{matrix} P = 4 π \frac{d^{2} R^{2}}{{(R - r)}^{2}} sin α cos α \sqrt[]{{(\frac{R - r}{d})}^{2} - sin^{2} α} . \end{matrix}

Mivel

P ≧ 0

, ezért

P

ugyanakkor maximális, amikor négyzetének pozitív konstans szorosa maximális. Elég tehát a

\begin{matrix} sin^{2} α cos^{2} α [{(\frac{R - r}{d})}^{2} - sin^{2} α] \end{matrix}

kifejezést vizsgálnunk, amely a

sin^{2} α = x

és

{(\frac{R - r}{d})}^{2} = a

jelöléssel a következő alakot ölti:

\begin{matrix} x (1 - x) (a - x) = x^{3} - (a + 1) x^{2} + a x . \end{matrix}

Az 1. ábráról leolvasható az a fontos észrevétel, hogy

\frac{R - r}{d} = sin β

ahol

β

a körök közös külső érintőinek az

O H

egyenessel alkotott hajlásszöge.
Hagyjuk most egy pillanatra figyelmen kívül

x

és a jelentését, és tekintsük a valós számokon értelmezett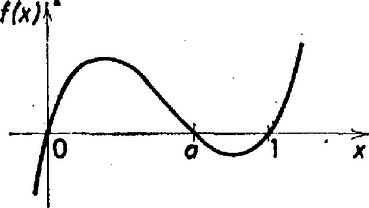

\begin{matrix} f (x) = x^{3} - (a + 1) x^{2} + a x \end{matrix}

függvényt, ahol

a

1-nél kisebb pozitív állandó. E függvénynek

3

valós zérus helye van, növekedő rendben:

x_{1} = 0

x_{2} = a

x_{3} = 1

. És mivel

x^{3}

együtthatója pozitív, ezért a függvény grafikonjának jellege a 2. ábra szerinti.

2. ábra

Mivel azonban feladatunkban

x = sin^{2} α

és

a = sin^{2} β

továbbá

0 ≦ α ≦ β

, azért e grafikonnak csak a

0

és

a

közé eső darabja ír le valóságos palástfelszín változást.
A felvetett kérdésre közel a válasz. Az

f (x)

függvény deriváltjának

0

és

a

közé eső zérushelyét kell megkeresnünk, abból

x = sin^{2} α

alapján a keresett szög meghatározható.

\begin{matrix} f' (x) = 3 x^{2} - 2 (a + 1) x + a, \end{matrix}

zérushelyei

\begin{matrix} x_{1} = \frac{a + 1 - \sqrt[]{a^{2} - a + 1}}{3} és x_{2} = \frac{a + 1 + \sqrt[]{a^{2} - a + 1}}{3} . \end{matrix}

Megmutatjuk, hogy

0 < x_{1} < a

, és hogy

x_{2} > a

. Az első állításhoz két irányból adunk becslést a gyökös kifejezésre:

egyrészt

\sqrt[]{a^{2} - a + 1} < \sqrt[]{a^{2} + 2 a + 1} = a + 1

,

másrészt

\sqrt[]{a^{2} - a + 1} = \sqrt[]{{(1 - a)}^{2} + a} > 1 - a (> 0)

.
A másodikhoz pedig

\begin{matrix} x_{2} > \frac{a + a + \sqrt[]{{(1 - a)}^{2} + a}}{3} > \frac{2 a + \sqrt[]{a}}{3} > a, \end{matrix}

hiszen

1 > a

. Ezek szerint

x_{1}

az a hely, amit keresünk.
Mindezek alapján a keresett szög:

\begin{matrix} x_{0} = Arc sin \sqrt[]{\frac{{(\frac{R - r}{d})}^{2} + 1 - \sqrt[]{{(\frac{R - r}{d})}^{4} - {(\frac{R - r}{d})}^{2} + 1}}{3}} . \end{matrix}

Arc sin y

(olvasd: arkusz szinusz főérték

y

) azt a (radiánban mért) a szöget jelenti, amelyre

sin α = y

és

- \frac{π}{2} ≦ α ≦ \frac{π}{2}

. (L. L.)

Károlyi Gyula (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)