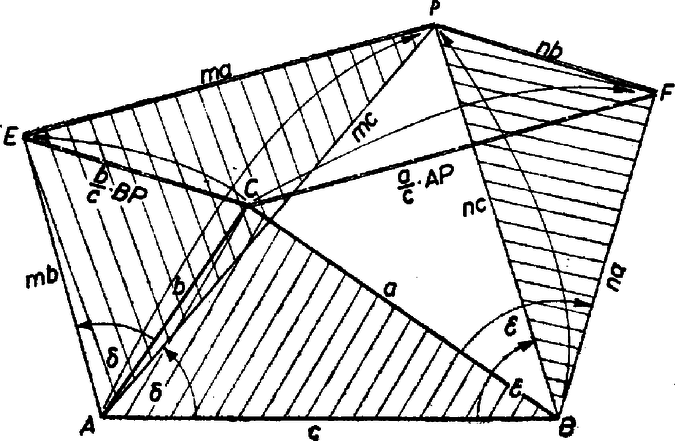
Felismerjük, hogy a vektorösszeadás szabálya értelmében azt kell bizonyítanunk, hogy a $PECF$ négyszög paralelogramma, egyik átlója a $PC$ eredő. Ezt a szemben levő oldalak egyenlőségéből igazoljuk.
Jelöljük az $ABC$ háromszög oldalait a szokás szerint, a két forgatva nyújtás irányított szögét rendre $BAP\sphericalangle =\delta$-val, $ABP\sphericalangle =\epsilon$-nal, a nyújtásaik (ill. zsugorításaik) arányszámát $m$-mel, $n$-nel.
Első transzformációnk az $ABC$ háromszöget a definíció szerint $APE$-be viszi át, és mivel $AP=m\cdot AB=mc$, valamint $AE=m\cdot AC=mb$, azért $PE=$ $=m\cdot BC=ma$, mert a forgatva nyújtás hasonlósági transzformáció, hiszen a forgatás is, a nyújtás is bármely idomot hozzá hasonló idomba visz át, az $APE$ képháromszög hasonló az $ABC$ háromszöghöz.
Hasonlók az $ABP$ és $ACE$ háromszögek is, mert $BAP\sphericalangle =CAE\sphericalangle =\delta$, és mert az $A$-ban összefutó oldalaik aránya $BAP:AP=1:m=CA:AE$. A megfelelő oldalpárok aránya $BA:CA=c:b$, ennélfogva harmadik oldalaikra $CE=\left(b/c\right)\cdot BP$.
Ugyanígy a második transzformáció alapján
$BPF\Delta \sim BAC\Delta$, $BP=n\cdot BA=nc$, $BF=n\cdot BC=na$ és $PF=n\cdot AC=$ $=nb$, továbbá
$BAP\Delta \sim BCF\Delta$, mert $ABP\sphericalangle =CBF\sphericalangle =\epsilon$ és $AB:BP=1:n=CB:BF$, a megfelelő oldalpárok aránya $AB:CB=c:a$, ennélfogva harmadik oldalaikra $CF=\left(a/c\right)\cdot AP$.
Összekapcsolva a megfelelő részeredményeket