Kezdőlap


Feladat:	F.2317	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ákosfai Z. , Alberti G. , Balázs Z. , Békési J. , Borsó Zs. , Böröczky K. , Csere K. , Cseri Hajnalka , Csörgő T. , Drávucz Katalin , Erdős 228 L. , Feledi György , Fóris Z. , Gulyás Gy. , Halász P. , Hatt J. , Hetyei G. , Hideg Sz. , Holbok I. , Ittzés A. , Jakab G. , Károlyi Gy. , Kerényi I. , Király Z. , Kovács 444 G. , Magyar Á. , Magyar Cs. , Megyesi G. , Mohay T. , Molnár L. , Nagy 548 R. , Regős Enikő , Simák Gy. , Szabó E. , Szijártó Z. , Terenyi Z. , Tóthegyi Tünde , Tranta Beáta , Törőcsik J. , Weisz F.
Füzet:	1982/január, 19 - 21. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Parabola egyenlete, Síkgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1981/május: F.2317

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha az állítás érvényes a $b$ egyenesre, akkor tetszőleges, $b$ -vel párhuzamos $b'$ egyenesre is igaz. Ugyanis a $b$ -t $b'$ -be vivő, rájuk merőleges eltolásvektor jellemzi a $B$ eltolódását is, a kérdéses $g$ egyenesét is, a forgó $e$ egyenes minden helyzetében (hacsak $A$ létrejön), tehát a $g$ egyenessereggel együtt a feladat állításában szereplő parabola is ugyanúgy tolódik el.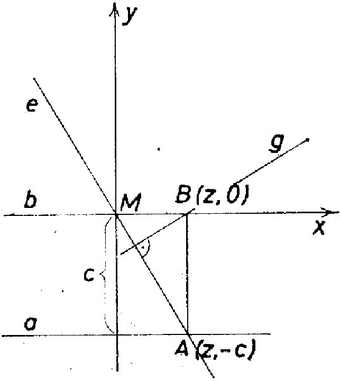
Vehetjük tehát $b$ helyére a vele párhuzamos, $M$ -en átmenő egyenest, tovább az egyszerűség kedvéért ezt jelöljük $b$ -vel. És vegyük mindjárt ezt derékszögű koordinátarendszerünk első tengelyéül, origójául $M$ -et, és ]egyen az $a$ egyenes egyenlete $y = - c$ , ahol $c > 0$ .

Jellemezzük

e

helyzetét az

a

-n futó

A (z, - c)

pontjával, ahol

z

paraméter. Nem jön létre

A

B

és

g

, ha

e ∥ a

, ha pedig

e ⊥ a

, azaz

z = 0

, akkor

g

azonos

b

-vel, hiszen ekkor

B = M

. Minden más esetben

e

és

g

iránytangense

- c / z

, ill.

z / c

, a

B

pont helyzete

(z, 0)

, ezekből

g

egyenlete

\begin{matrix} \frac{y}{x - z} = \frac{z}{c}, y = \frac{z}{c} x - \frac{z^{2}}{c} . \end{matrix}

(1)

Ebben az eredményben benne van az előre elintézett

z = 0

eset is.
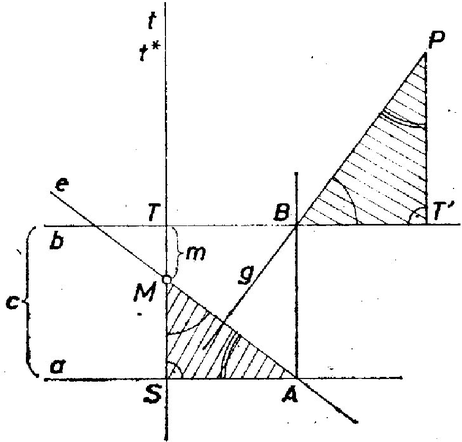
A kapott egyenlet pedig azonos az

y = \frac{x^{2}}{4 c}

parabolához a

(2 z, \frac{z^{2}}{c})

pontjában húzott érintő egyenletével. Ugyanis az érintő iránytangense deriválás útján bármely

x_{0}

pontban

\frac{x_{0}}{2 c}

, tehát egyenlete

\begin{matrix} \frac{y - \frac{x_{0}^{2}}{4 c}}{x - x_{0}} = \frac{x_{0}}{2 c}, \end{matrix}

ill.

x_{0} = 2 z

mellett

\begin{matrix} \frac{y - \frac{z^{2}}{c}}{y - 2 z} = \frac{z}{c}, \end{matrix}

átrendezve valóban azonos (1)-gyel.

Ezzel az állítást bebizonyítottuk.
A

c > 0

kikötés nem volt lényeges, csak a szemléletesség, az ábrával való egyezés kedvéért alkalmaztuk; a feladat szerint mindenesetre

c \neq 0

II. megoldás. Előkészítésül fel fogjuk használni a parabola következő tulajdonságát. Legyen a parabola tengelye

t

, csúcsa

C

, az itt húzott érintője

c

, továbbá egy tetszőleges

P

pontjához tartozó érintőjének

c

-vel,

t

-vel való metszéspontja

Q

, ill.

R

, ekkor

Q

felezi a

P R

szakaszt. Ekvivalens ezzel, hogy

Q

felezi a

C P'

szakaszt, ahol

P'

P

-nek

c

-n levő vetülete.
Jelöljük

t^{*}

-gal az

M

-en átmenő,

a

-ra merőleges egyenest. Erre tengelyesen szimmetrikus a kiindulási

a

b

M

alakzat, és ezért

t^{*}

a forgó

e

egyenesből leszármaztatott

g

egyenesek seregének is szimmetriatengelye, tehát az állítás szerinti parabola tengelye csak

t^{*}

lehet. (Ha ugyanis

e

-nek

e_{1}

és

e_{2}

helyzetei egymás képei

t^{*}

-ra, akkor ugyanez áll a megfelelő

A_{1}

- és

A_{2}

-re,

B_{1}

- és

B_{2}

-re,

M A_{1}

-re és

M A_{2}

-re, tehát

g_{1}

és

g_{2}

-re is.) Tovább

t^{*}

helyett a

t

jelet írjuk.
Jelöljük

t

-nek

a

-n,

b

-n levő pontját

S

-sel,

T

-vel, a

T

-nek

B

-re való tükörképét

T'

-vel, továbbá

P

-vel a

g

-nek azt a pontját, amelyre

P T'

merőleges

b

-re. Belátjuk, hogy

P

mértani helye egy parabola. (

P

létezik, ha

g

létrejött.) Szerkesztésünk alapján

B P T'

és

M A S

hasonló (derékszögű) háromszögek, ebből

\begin{matrix} P T' = \frac{B T'}{M S} \cdot A S = \frac{T T'^{2}}{4 M S}, \end{matrix}

(2)

hiszen

A S = B T = B T' = T T' / 2

. Ha pedig speciálisan

e

merőleges

a

-ra, vagyis azonos

t

-vel, akkor

A = S

B = T

g = b

és

P = T

, tehát (2) érvényes erre az esetre is.
A

b

t

egyenespárt a derékszögű koordináta‐rendszer első, ill. második tengelyének véve (2) így alakul:

\begin{matrix} y = \frac{x^{2}}{4 M S}, \end{matrix}

(2a)

ami valóban parabola egyenlete.
Azt kell még belátnunk az állítás igazolásához, hogy a (2a) parabolához

P

-ben fektetett érintő éppen a felhasznált

g

egyenes.

Mivel a parabola tengelye az

S T

egyenes, s tengelypontja a

T

pont, azért ez az érintő ‐ közismerten ‐ átmegy

T T'

felezőpontján, azaz a

B

ponton. Ám a

g

egyenes is ilyen, hiszen úgy vettük fel, hogy átmenjen

B

ponton, és a

P

pontot rajta vettük fel. Így ‐ mivel a

P

pontban a parabolához csak egy érintő húzható, s ennek tulajdonságaival a

g

egyenes rendelkezik, ezért a fent megadott parabolát a

g

minden

P

esetén a

P

pontban érinti. És bármely

g

ugyanazt a fent megadott parabolát érinti, mivel a parabola adatai az

e

egyenestől ‐ és így a

P

ponttól ‐ függetlenek.