Kezdőlap


Feladat:	F.2306	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Böröczky K. , Csere K. , Heckenast L. , Heckenast László , Károlyi Gyula
Füzet:	1981/december, 196 - 198. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül körökben, Koszinusztétel alkalmazása, Körérintési szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1981/március: F.2306

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a feladat szövege a feladatban szereplő félköröknek csak az átmérőjét írja elő, egyelőre tekintsük az $A A_{1}$ és $B B_{1}$ átmérőjű köröket (és persze az AB negyedkörívet) azoknak az alakzatoknak, amelyeket érintenie kell a keresett körnek. A továbbiakban az $A A_{1}$ , ill. $B B_{1}$ átmérőjű köröket jelölje $k_{A}$ , ill. $k_{B}$ , a keresett kört pedig $k$ . Ha $k$ kívülről érintené az $A B$ ívet, vagy az $A B$ ív érintené belülről $k$ -t, akkor $k$ -nak $A$ -ban és $B$ -ben egyidejűleg kellene érintenie az $A B$ ívet, mivel $k_{A}$ és $k_{B}$ az $A B$ ívet tartalmazó kör belsejében vannak. Ilyen feltételek mellett $k$ csak maga az $A B$ ívet tartalmazó kör lehetne. Két körív azonossága esetén viszont nem mondjuk azokat érintkezőknek.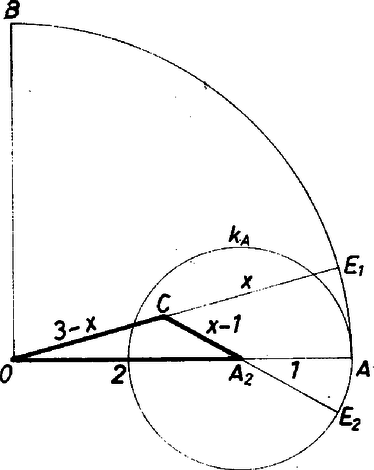
Tehát $k$ , belülről érinti az $A B$ ívet, és $k_{A}$ , $k_{B}$ és $k$ kölcsönös elhelyezkedését illetően a következő lehetőségek vannak: $k_{A}$ és $k_{B}$ érinthetik $k$ -t 1. mindketten belülről, 2. mindketten kívülről, 3. egyikük belülről, másikuk kívülről. Mivel az adott körök az $A O B$ szög szögfelezőjére nézve szimmetrikusan helyezkednek el, az első esetben $k$ középpontja is az $A O B$ szög szögfelezőjén van, a harmadik esetben pedig az $O A$ vagy az $O B$ szögszáron van $k$ középpontja aszerint, hogy $k_{A}$ vagy $k_{B}$ érinti-e $k$ -t belülről.
Érintse ugyanis $k$ -t pl. $k_{A}$ belülről (1. ábra).

1. ábra

Jelölje

k

középpontját

C

, sugarát

x

, az

A B

ív és

k

érintési pontját

E_{1}

k

és

k_{A}

érintési pontját

E_{2}

k_{A}

középpontját

A_{2}

. Mivel

O C = 3 - x

C A_{2} = x - 1

O A_{2} = 2

, ezért

O C + C A_{2} = O A_{2}

. Az

O C A

háromszög elfajuló, tehát

C

O A

egyenesen van.
A harmadik esetben mondottak az első esetre kétszeresen is alkalmazhatók, ezért az első esetben

k

középpontja csak

O

lehetne. Mivel azonban magát az

A B

ívet tartalmazó kört nem tekintjük megoldásnak, az első lehetőséget elvetjük.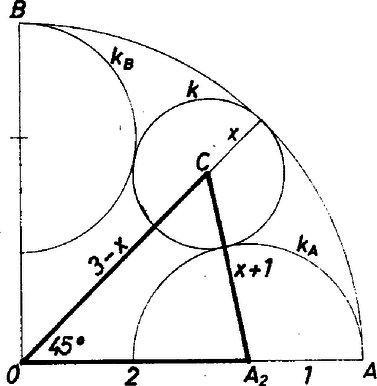

2. ábra

A második esetben (2. ábra) a

k

kör sugarát

x

-szel jelölve a koszinusz-tétel szerint

\begin{matrix} {(1 + x)}^{2} = 4 + {(3 - x)}^{2} - 4 (3 - x) cos 45^{\circ} \end{matrix}

ahonnan

\begin{matrix} x = \frac{6 - 3 \sqrt[]{2}}{4 - \sqrt[]{2}} = \frac{9 - 3 \sqrt[]{2}}{7} \approx 0, 6796. ... \end{matrix}

3. ábra

A harmadik esetben az

O B_{2} C

derékszögű háromszögben (3. ábra)

\begin{matrix} {(1 + x)}^{2} = 4 + {(3 - x)}^{2}, \end{matrix}

ahonnan

\begin{matrix} x = 1, 5. \end{matrix}

Tehát a harmadik esetben a keresett kör középpontja az

O A

, ill.

O B

szakaszok felezőpontja lehet. Megállapodás dolga, hogy ezeket megoldásnak tekintjük-e, hiszen az érintési pontok ebben az esetben a feladatban szereplő körívek végpontjai.
Foglalkoznunk kell még a második esetben

k

középpontjának megszerkesztésével. Növeljük meg

k

sugarát az egységgel. Az így kapott kör átmegy a

k_{A}

kör

A_{2}

és a

k_{B}

kör

B_{2}

középpontján, továbbá az

A O B

szög szögfelezőjén levő, az

O

-tól 4 egységnyire fekvő

D

ponton (4. ábra).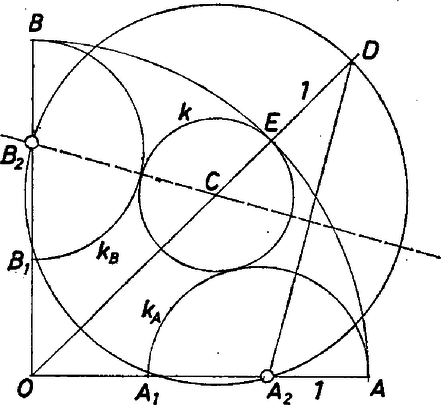

4. ábra

A_{2} B_{2} D

háromszög köré írható kör középpontját kell tehát megszerkesztenünk. Az így kapott

C

pontnak az

O D

egyenes és az

A B

negyedkörív

E

metszéspontjától való távolsága a keresett kör sugara.

Heckenast László (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)