Kezdőlap


Feladat:	F.2281	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1981/április, 155 - 157. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1980/november: F.2281

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a rögzített kör sugara a hosszúságegység, középpontja a koordináta-rendszer origója, a másik kör centruma a $C (c, 0)$ pont és sugara $r$ . A követelményekre tekintettel 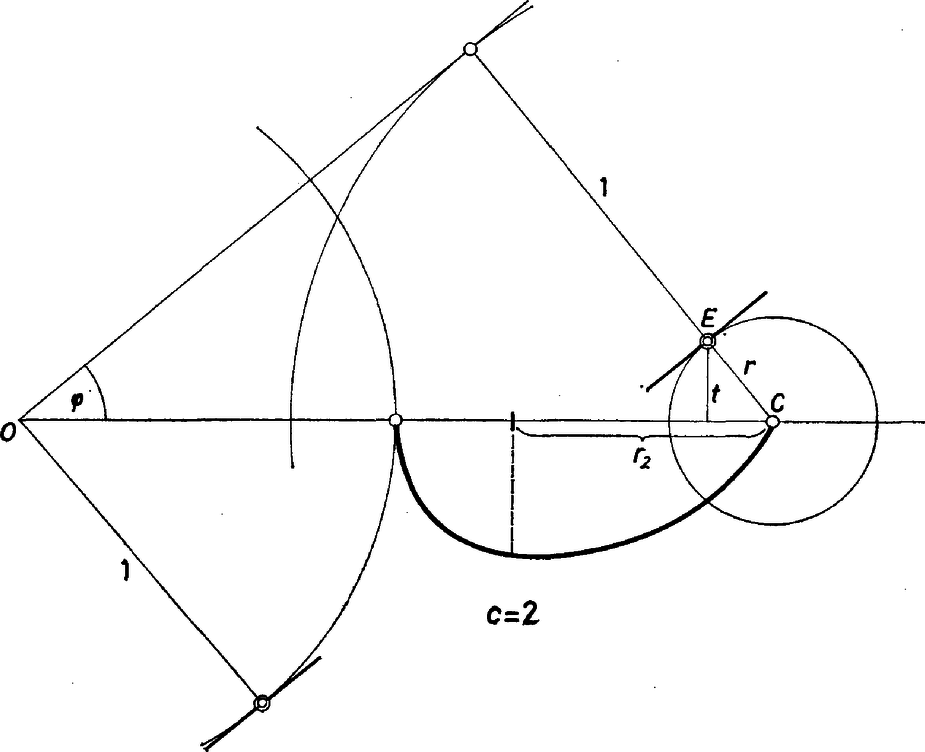$c > 1$ és $0 \leq r \leq c - 1$ .

Ekkor a belső közös érintők egyikének

φ

irányszögére ‐ az irány ismert szerkesztési elve szerint ‐

\begin{matrix} s i n φ = \frac{1 + r}{c}, cos φ = \frac{1}{c} \sqrt[]{c^{2} - {(1 + r)}^{2}} . \end{matrix}

Ebből a kérdéses

E

érintési pontnak

O C

-től való távolsága

\begin{matrix} t = r sin (90^{\circ} - φ) = \frac{r}{c} \sqrt[]{c^{2} - {(1 + r)}^{2}} . \end{matrix}

Ez nem negatív, ezért elég megkeresnünk

t^{2}

maximumát:

\begin{matrix} t^{2} = \frac{c^{2} - 1}{c^{2}} r^{2} - \frac{2}{c^{2}} r^{3} - \frac{1}{c^{2}} r^{4} . \end{matrix}

Keressük, hol tűnik el a deriváltja. Ez, mindjárt átrendezés után:

\begin{matrix} (- \frac{2 r}{c^{2}}) (2 r^{2} + 3 r - c^{2} + 1) = 0. \end{matrix}

Az első tényező révén

r = 0

mellett teljesül ez, de mi nem ezt keressük, hiszen itt

t = 0

.
A nagy zárójelbeli másodfokú polinomnak két különböző zérushelye van:

r_{1}

r_{2}

-ben, hiszen

r_{1} r_{2} = - (c^{2} - 1) / 2 < 0

, előjelük különböző; legyen

r_{1} < 0 < r_{2}

. Így

r_{1}

nincs benne

t

értelmezési tartományában,

\begin{matrix} r_{2} = - \frac{3}{4} + \sqrt[]{\frac{c^{2}}{2} + \frac{1}{16}} \end{matrix}

viszont benne van, mert a tartomány jobb végpontjában,

(c - 1)

-ben már pozitív a polinom értéke:

c^{2} - c = c (c - 1) > 0

(és mert a másodfokú tag együtthatója pozitív).
Az

r_{2}

helyen növekedve halad át a polinom, tehát a derivált csökkenően. Eszerint ott

t^{2}

-nek maximuma van, és vele együtt

t

-nek is. Ezzel a feladatot megoldottuk.