| Feladat: | F.2210 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1979/november, 143. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Indirekt bizonyítási mód, Kombinatorikus geometria síkban, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1979/május: F.2210 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Nincs mit bizonyítani, ha az adott pontok száma vagy . Akkor sem kell viszont -nél több pontot egyidejűen tekintetbe vennünk, ha több pontunk van, hiszen pont határoz meg összekötő szakaszt, ha nincs közös végpontjuk (különben közös végpontra úgysem vonatkozik az állítás). És ha nem volna igaz az állítás, vagyis lehetne mutatni olyan (nem az adottak közül való) pontot, amely több szakasznak közös belső pontja, ehhez a cáfolathoz is elég lenne mutatni kettőt a -n átmenő szakaszok közül. 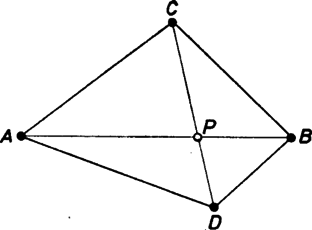 Föltevéseink szerint és , ennélfogva
Eszerint a pont létezéséből levont két helyes következtetés nem egyeztethető össze, feltételezésünk tehát hibás volt. Ezzel meggyőződtünk arról, hogy az állítás igaz. Megjegyzés. (2)-ben az egyenlőségek megengedését elkerülhettük volna további meggondolások árán, de a megengedés úgysem érinti az ellentmondást, mert (1)-ben szigorú egyenlőtlenség érvényes a föltevések alapján. |