Kezdőlap


Feladat:	F.2167	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/február, 66. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Két pont távolsága, szakasz hosszúsága, Feladat
Hivatkozás(ok):	Feladatok: 1978/október: F.2167

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C D$ pontrendszerben az $A C$ és $B D$ egyenesek merőlegesek, így $M$ metszéspontjuknál $4$ derékszögű háromszög keletkezik. Az $A B$ és $C D$ átfogók négyzetét Pitagorasz tétele szerint fölírva, az $A M$ , $B M$ , $C M$ és $D M$ befogók négyzetét $1$ -szer‐ $1$ -szer használjuk föl, és ugyanez áll a másik átfogópár: $B C$ és $D A$ négyzetében; ennélfogva

\begin{matrix} A B^{2} + C D^{2} = B C^{2} + D A^{2} . \end{matrix}

A vesszős pontnégyes oldalaira közölt egyenlőségek szerint abban is teljesül

\begin{matrix} A' B'^{2} + C' D'^{2} = B' C'^{2} + D' A'^{2} . \end{matrix}

(1)

Tegyük koordináta-rendszerünk

x

tengelyét az

A' C'

egyenesre, és legyenek pontjaink koordinátái:

A' (a, 0)

B' (x_{1}, y_{1})

C' (c, 0)

D' (x_{2}, y_{2})

. Ezekkel (1)-ből:

\begin{matrix} {(x_{1} - a)}^{2} + y_{1}^{2} + {(x_{2} - c)}^{2} + y_{2}^{2} = {(x_{1} - c)}^{2} + y_{1}^{2} + {(x_{2} - a)}^{2} + y_{2}^{2}, \end{matrix}

rendezés után

\begin{matrix} (a - c) (x_{2} - x_{1}) = 0. \end{matrix}

Mivel

A'

és

C'

különböző pontok (különben az

A' C'

egyenes határozatlan), azért

a - c \neq 0

, tehát

x_{2} - x_{1} = 0

, azaz

x_{2} = x_{1}

. Eszerint a

B' D'

egyenes párhuzamos az

y

tengellyel, vagyis merőleges

A' C'

-re. Ezt kellett bizonyítanunk.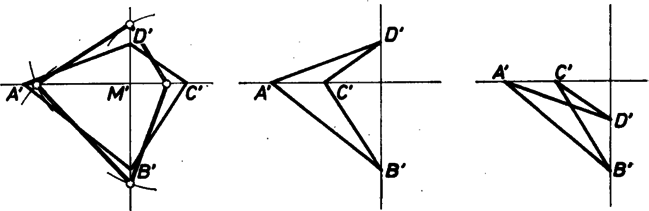

Megjegyzés. Látjuk, hogy az átlók merőlegessége kapcsolatban áll az oldalak négyzetösszegéből képezhető

A B^{2} - B C^{2} + C D^{2} - D A^{2}

kifejezés

0

-értékével. Eszerint a négy oldal és a két átló közti szög ‐ mint

5

adat ‐ nem független egymástól, együtt nem elég a négyszög meghatározására. Valóban, az ábra változatai mutatják, hogy több alak is lehetséges ugyanabból a négy szakaszból.