Kezdőlap


Feladat:	F.1815	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1972/november, 143 - 145. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Kör egyenlete, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1972/március: F.1815

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Könnyű látni a koordinátákból, hogy $C$ ugyanakkora távolságra van az $O$ origótól, mint $A$ és $B$ , tehát a $k$ körülírt kör egyenlete

\begin{matrix} x^{2} + y^{2} = 25. \end{matrix}

(1)

Jelöljük

P

koordinátáit (

u

v

)-vel,

A

-éit (

x_{A}

y_{A}

)-val, így (1) alapján

\begin{matrix} P A^{2} = {(u - x_{A})}^{2} + {(v - y_{A})}^{2} = (u^{2} + v^{2}) - 2 x_{A} u - 2 y_{A} v + (x_{A}^{2} + y_{A}^{2}) = \\ = 2 \cdot 25 - 2 x_{A} u - 2 y_{A} v, \end{matrix}

hiszen

P

és

A

koordinátái egyaránt kielégítik (1)-et.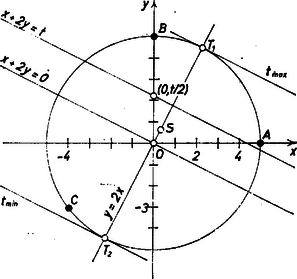

Hasonlóan fejezhető ki

P B^{2}

és

P C^{2}

B (x_{B}, y_{B})

és

C (x_{C}, y_{C})

koordinátákkal, és így a vizsgálandó négyzetösszeg:

\begin{matrix} f (P) = 150 - 2 (x_{A} + x_{B} + x_{C}) u - 2 (y_{A} + y_{B} + y_{C}) v \end{matrix}

akkor és csak akkor minimális, ha az

\begin{matrix} (x_{A} + x_{B} + x_{C}) u + (y_{A} + y_{B} + y_{C}) v \end{matrix}

(2)

kifejezés értéke, ami a mi esetünkben

u + 2 v

, maximális, azzal a mellékföltétellel, hogy (

u

v

) rajta van

k

-n, azaz

u^{2} + v^{2} = 25

.
Mármost az

u + 2 v

kifejezés értéke adott

c

esetén az

\begin{matrix} x + 2 y & = c, másképpen & (3) \\ y & = - \frac{1}{2} x + \frac{c}{2} \end{matrix}

egyenletű

e

egyenes pontjaira állandó, és

e

-t párhuzamosan eltolva csak

c

értéke változik meg. Az egyenes átmegy az

y

tengely

(0; \frac{c}{2})

pontján, és

c

növelése egyértelmű azzal, hogy ez a pont fölfelé tolódik a tengelyen.

c

értékét azonban csak addig növelhetjük, míg (3)-nak van közös pontja az (1) körrel és

c

legnagyobb lehetséges értéke akkor adódik, ha a (3) egyenes érinti

k

-t. A

T

érintési pontot a kör középpontjából

e

-re bocsátott merőleges metszi ki

k

-ból. A merőleges egyenlete

y = 2 x

, ennek

k

-val közös pontjai:

\begin{matrix} T_{1} (\sqrt[]{5}, 2 \sqrt[]{5}), T_{2} (- \sqrt[]{5}, - 2 \sqrt[]{5}), \end{matrix}

és

u + 2 v

nyilvánvalóan a

T_{1}

-ben veszi fel legnagyobb, (

c = 5 \sqrt[]{5}

) értékét, tehát (2) itt a legkisebb, ez a keresett

P

pont. (

T_{2}

-ben viszont maximális

f (P) = f (T_{2})

értéke.)

Megjegyzések. 1. A (2) kifejezés így írható:

3 x_{S} u + 3 y_{S} v

, ahol (

x_{S}

y_{S}

) az

A B C

háromszög

S

súlypontjának koordinátái. Ebből az észrevételből a fentiekhez hasonlóan adódik, hogy bármely, a

k

-ba beírt

A B C

háromszög csúcsaira képezve az

f (P) = P A^{2} + P B^{2} + P C^{2}

összeget, ez az

O S

sugár (félegyenes) által

k

-ból kimetszett

P

pontra lesz minimális értékű ‐ más szóval

k

-nak az

S

-hez legközelebbi

P

pontjára ‐, az átellenes pontra pedig maximális.

S

akkor és csak akkor azonos

O

-val, ha az

A B C

háromszög egyenlő oldalú, ebben az esetben a

k

-n körülfutó

P

-re

f (P)

állandó (akárcsak bármely páros oldalszámú szabályos sokszög esetében).
Az

O S

egyenest a háromszög Euler‐féle egyenesének nevezik. Ismeretes, hogy ‐ ha létezik ‐ átmegy a magasságponton is, valamint a háromszög középháromszöge és egyben a talpponti háromszöge köré írt (Feuerbach‐féle) kör középpontján is. A fenti eredménnyel az Euler‐egyenesnek egy újabb tulajdonságát ismertük meg.
2. Az

f (P)

kifejezés számértéke arányos az

A

B

C

tömegpontrendszer tehetetlenségi nyomatékával, a

P

-n átmenő és

k

síkjára merőleges forgástengelyre vonatkozóan, amennyiben

A

B

C

mindegyikébe egyenlő tömeget helyezünk el. Eredményünk pedig a mechanika ún. Steiner‐tételének megfelelője: ha egy

M

össztömegű pontrendszer tehetetlenségi nyomatéka egy, a rendszer

S

súlypontján átmenő

t

tengelyre

K_{0}

, akkor, egy a

t

-vel párhuzamos, tőle

d

távolságban levő

t'

tengelyre

K = K_{0} + M d^{2}

, tehát

K

t

-re minimális, és

d

akkor a legkisebb, ha

k

-nak

S

-hez legközelebbi pontján át vesszük fel

t'

-t.
Erre a kapcsolatra több dolgozat helyesen rámutatott. Az viszont már nagy kerülő, ha a kérdést ezen az úton kívánjuk megválaszolni, hiszen az idézett tétel maga is matematikai meggondolások eredménye.