Kezdőlap


Feladat:	F.1795	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kovács István
Füzet:	1974/november, 109 - 114. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Forgatva nyújtás, Parabola egyenlete, Kúpszeletek érintői, Mértani helyek, Parabola, mint kúpszelet, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1971/november: F.1795

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladatot koordináta-geometriai módszerrel oldjuk meg. A koordináta-rendszert úgy választjuk meg, hogy az adott parabola egyenlete $y = x^{2}$ legyen. Ekkor a parabola $d$ vezéregyenesének egyenlete $y = - \frac{1}{4}$ . Egy $P (u, v)$ fókuszú, $d$ -vel párhuzamos vezéregyenesű parabola egyenlete, amennyiben a vezéregyenes és fókusz távolsága $s$ , vagy

\begin{matrix} y = \frac{1}{2 s} {(x - u)}^{2} + v - \frac{s}{2}, \end{matrix}

(1)

vagy pedig

\begin{matrix} y = - \frac{1}{2 s} {(x - u)}^{2} + v + \frac{s}{2}, \end{matrix}

(2)

aszerint, hogy a parabola fókusza a vezéregyenes ,,felett'' vagy ,,alatt'' helyezkedik el (1. ábra).

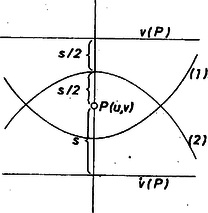1. ábra

Vizsgáljuk meg, hogy mely

P (u, v)

pontok esetén fogja az (1) parabola érinteni az

y = x^{2}

parabolát.
Két görbe akkor érinti egymást, ha van közös pontjuk, és a két görbéhez abban a pontban húzott érintők egybeesnek (2. ábra).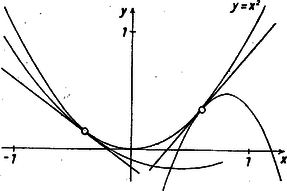

2. ábra

Ha a két parabola érinti egymást az

x

abszcisszájú pontban, akkor az abban a pontban húzott érintők iránytangenseinek meg kell egyeznie. És fordítva: ha ezek megegyeznek, akkor a két görbe érinti egymást.
Az

y = x^{2}

görbéhez az

x

abszcisszájú pontban húzott érintő iránytangense

y' = 2 x

; az (1) görbéhez húzott érintő iránytangense

y' = \frac{1}{s} (x - u)

. Ennek a két értéknek kell megegyeznie:

\begin{matrix} 2 x = \frac{1}{s} (x - u), \\ (1 - 2 s) x = u . & (3) \end{matrix}

Ha már most

2 s \neq 1

, akkor ebből

x = u / (1 - 2 s)

, azaz csak az ilyen abszcisszájú pontban érintheti egymást a két parabola. Ha viszont az

x = u / (1 - 2 s)

pontban a paraboláknak közös pontja van, akkor ott érintik is egymást. Tehát

(2 s - 1) \neq 0

esetén a két parabola csak akkor érinti egymást, ha

\begin{matrix} {(\frac{u}{1 - 2 s})}^{2} = \frac{1}{2 s} {(\frac{u}{1 - 2 s} - u)}^{2} + v - \frac{s}{2}, \end{matrix}

azaz ha

u

és

v

között a

\begin{matrix} v = \frac{1}{1 - 2 s} \cdot u^{2} + \frac{s}{2} \end{matrix}

(4)

összefüggés áll fenn.
Ha viszont

2 s = 1

, akkor (3) csak úgy állhat fenn, ha

u = 0

, ekkor viszont az (1) parabolaegyenlet

y = x^{2} + v - \frac{1}{4}

alakú lesz. Így

2 s - 1 = 0

esetén az (1) parabola, valamint az

y = x^{2}

parabola

v \neq \frac{1}{4}

mellett nem érinti egymást,

v = \frac{1}{4}

mellet pedig azonosak; innen nem kapunk megoldást.
Hasonlóan azt vizsgálva, hogy a (2) parabola és az

y = x^{2}

parabola mikor érinti egymást, a

2 x = - \frac{1}{s} (x - u)

-ból az

x = u / (2 s + 1)

abszcisszájú pontban lehet csak érintés, és ez

2 s + 1 \geq 1

miatt mindig értelmes. Így a (2) parabola és az

y = x^{2}

parabola csak akkor érinti egymást, ha

\begin{matrix} {(\frac{u}{2 s + 1})}^{2} = - \frac{1}{2 s} {(\frac{u}{2 s + 1} - u)}^{2} + v + \frac{s}{2}, \end{matrix}

vagyis ha

\begin{matrix} v = \frac{1}{1 + 2 s} \cdot u^{2} - \frac{s}{2} \end{matrix}

(5)

Összefoglalva, a

P (u, v)

ponthoz akkor és csak akkor találunk a feladatban előírt tulajdonságú parabolát, ha (5) teljesül, vagy ha

2 s - 1 \neq 0

és (4) teljesül. Így a keresett mértani hely

2 s - 1 \neq 0

esetén az

\begin{matrix} y = \frac{1}{1 + 2 s} \cdot x^{2} - \frac{s}{2}, \end{matrix}

'

)

és az

\begin{matrix} y = \frac{1}{1 - 2 s} \cdot x^{2} + \frac{s}{2} \end{matrix}

'

)

egyenletek valamelyikét kielégítő pontok (két parabola), míg

2 s - 1 = 0

esetén csak az

\begin{matrix} y = \frac{x^{2}}{2} - \frac{1}{4} \end{matrix}

''

)

egyenletet kielégítő pontok (egy parabola).
Megvizsgáljuk, hogyan származnak a kapott parabolák az

y = x^{2}

parabolából és az adott

s

szakaszból. Az adott parabola csúcsa a

(0; 0)

pont, fókusza

F (0; \frac{1}{4})

, vezéregyenese ‐ mint már mondtuk ‐ az

y = - \frac{1}{4}

egyenes; a (4

'

) parabola csúcsa

(0; \frac{s}{2})

‐ ahol

s \neq \frac{1}{2}

‐, paraméternek fele

\begin{matrix} \frac{1}{4} | \frac{1}{\frac{1}{1 - 2 s}} | = | \frac{1}{4} - \frac{s}{2} | . \end{matrix}

Mármost, ha

0 < 2 s < 1

, akkor (4

'

) fókuszának ordinátája:

\frac{s}{2} + (\frac{1}{4} - \frac{s}{2}) = \frac{1}{4}

, vagyis e fókusz azonos

F

-fel; vezéregyenese pedig az

\begin{matrix} y = \frac{s}{2} - (\frac{1}{4} - \frac{s}{2}) = - \frac{1}{4} + s \end{matrix}

egyenes, a kiindulási parabola vezéregyenesének eltoltja

s

-sel (fölfelé). Mivel ekkor még

s < 1 / 2

, azért a föltolt vezéregyenes még alatta van

F

-nek, fölfelé nyílik a parabola.
Ha viszont

2 s > 1

, azaz

s / 2 > 1 / 4

, akkor (4

'

) csúcsa az

F

fölött van (egyszersmind

x^{2}

együtthatója negatív), a parabola lefelé nyílik, fókusza lejjebb van, mint a csúcs. E fókusz ordinátája

\begin{matrix} \frac{s}{2} - | \frac{1}{4} - \frac{s}{2} | = \frac{s}{2} - (\frac{s}{2} - \frac{1}{4}) = \frac{1}{4}, \end{matrix}

tehát ekkor is azonos

F

-fel, vezéregyenese

y = - \frac{1}{4} + s

, ekkor is

s

-sel van föltolva. (De ekkor túl van tolva az

F

-en.) A kizárt

2 s = 1

eset pedig azt jelentené, hogy az

y = x^{2}

parabola vezéregyenesét rátolnánk a fókuszára; emiatt nem keletkezik ilyenkor

P

mértani helye az (1) alakból.
Hasonlóan látható ‐ de egyszerűbben ‐, hogy (5

'

) csúcsa minden pozitív

s

-re a

(0; - s / 2)

pont, fókusza

F

, vezéregyenese

y = - 1 / 4 - s

, vagyis lefelé van eltolva

s

-sel.

II. megoldás. A feladatot koordináta-rendszer alkalmazása nélkül is megoldjuk. A megoldásban felhasználjuk azt a tényt, hogy a parabola érintője felezi az érintési pontot a fókusszal összekötő egyenes, valamint az érintési pontból a vezéregyenesre emelt merőleges szögét.
Legyen az adott parabola fókusza

F

, a fókusz és a

d

vezéregyenes közti távolság

p

. Tegyük fel, hogy a

P

fókuszú,

v

vezéregyenesű parabola a megadott parabolát az

E

pontban érinti, azaz a két parabolához

E

pontban közös,

e

érintő húzható. Mivel a feltétel szerint

v

és

d

párhuzamos, ezért az

E

pontból

v

-re, illetve

d

-re bocsátott merőlegesek

T_{1}

, illetve

T_{2}

talppontjai és az

E

pont egy egyenesen vannak.
Két esetet különböztetünk meg aszerint, hogy a

T_{1} T_{2}

szakasz belsejében tartalmazza az

E

pontot vagy sem.
I. Ha

E

T_{1} T_{2}

szakasz belső pontja, akkor

F

és

P

e

egyenes különböző oldalára esik, azaz

F P = F E + E P

. A

P T_{1} C_{1}

és az

F T_{2} C_{2}

háromszögek (lásd a 3. ábrát) hasonlóak, mert megfelelő oldalaik párhuzamosak.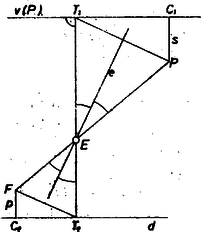

3. ábra

Hasonlóságuk aránya

P C_{1} : F C_{2} = s : p

. Hasonlók a

P E T_{1}

, valamint

F E T_{2}

háromszögek is, hasonlóságuk aránya

P T_{1} : F T_{2} = s : p

, azaz

E P : F E = s : p

, ahonnan

\begin{matrix} \frac{F P}{F E} = \frac{F E + E P}{F E} = 1 + \frac{E P}{F E} = 1 + \frac{s}{p} . \end{matrix}

Így a

P

pontot az

E

pontból

F

középpontú,

(1 + \frac{s}{p})

arányú nagyítással kapjuk. Ez azt jelenti, hogy a keresett tulajdonságú

P

pontok rajta vannak az eredeti parabola

F

középpontú

, (1 + \frac{s}{p})

arányú nagyítottján.
Megmutatjuk, hogy ennek a parabolának összes pontja rendelkezik azzal a tulajdonsággal, hogy egy alkalmas parabolának fókusza.
Legyen ugyanis

P

a nyújtott parabola egy pontja. Mivel

P

az eredeti parabola egy

E

pontjának képe, azért

F P : F E = 1 + \frac{s}{p}

és

F

E

P

ilyen sorrendben vannak az egyenesen, tehát

E P : E F = s : p

.
Legyen továbbá

E

merőleges vetülete

d

-re

T_{2}

F

merőleges vetülete

C_{2}

és tükrözzük

E

-re az

F C_{2} T_{2}

háromszöget, majd nyújtsuk meg

s / p

-szeresére. Az

F

pont ekkor a

P

pontba fog átmenni, a

T_{2}

, illetve

C_{2}

pontok pedig

T_{1}

, illetve

C_{1}

pontokba.

T_{1} C_{1}

párhuzamos lesz

T_{2} C_{2}

-vel, hiszen a tükrözés és hasonlóság párhuzamosságtartó, továbbá

E P = E T_{1}

, hiszen ez az egyenlő szárú

F E T_{2}

háromszög tükrözöttje, illetve nagyítottja.

P C_{1} = \frac{s}{p} \cdot F C_{2} = \frac{s}{p} \cdot p = s

, vagyis az

E

pont rajta van a

P

fókuszú,

T_{1} C_{1}

vezéregyenesű parabolán, és

P

, valamint

T_{1} C_{1}

távolsága éppen

s

. Másrészt

F

E

P

, valamint

T_{2}

E

T_{1}

egy egyenesre esnek, azért mind a két parabolához az

E

pontban húzott érintő ugyanaz, az

F E T_{2}

szög vagy a

P E T_{1}

szög szögfelezője.
Így beláttuk, hogy a feladatbeli mértani hely ‐ abban az esetben, ha

T_{1} T_{2}

szakasznak az

E

pont belső pontja ‐ a megadott parabolának

F

középpontú,

1 + s / p

arányú nagyítottja.
II. Ez az eset hasonló az előzőhöz, azért itt csak utalunk az egyes lépésekre (4. ábra).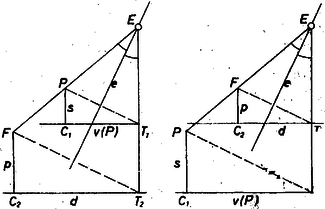

4. ábra

F

, valamint

P

pontok az

e

egyenesnek ugyanarra a partjára esnek, így irányított szakaszokat nézve

F P = F E - P E

. A

P T_{1} C_{1}

, valamint az

F T_{2} C_{2}

háromszögek, majd a

P E T_{1}

és

F E T_{2}

háromszögek hasonlóságából

P E : F E = s : p

, ahonnan

\begin{matrix} \frac{F P}{F E} = \frac{F E - P E}{F E} = 1 - \frac{s}{p} \end{matrix}

pozitív arány esetén, ez egy

F

középpontú, adott arányú hasonlósági transzformációt jelent, ha negatív, akkor még egy

F

pontra vonatkozó tükrözést is. Amennyiben az arány nulla, úgy azt kapjuk, hogy a két parabola fókusza, vezéregyenese egybeesik, tehát a két parabola is egybeesik, ekkor viszont nem érintik egymást.
Így a második esetben a mértani hely

s \neq p

esetén az adott parabola

F

középpontú,

(1 - \frac{s}{p})

arányú nagyítottja. Most is az előzőekhez hasonlóan meg lehet mutatni, hogy ennek a megnyújtott parabolának minden pontja eleme a mértani helynek.

s = p

esetben pedig megfelelő pont nincs.
Összefoglalva: ha

s \neq p

, akkor a keresett mértani hely a megadott parabola

F

középpontú,

1 + s / p

, illetve

1 - s / p

arányú nagyítottjainak uniója. Ha

s = p

, akkor az eredeti parabola

F

középpontú,

2

-szeres nagyítottja.

Kovács István (Budapest, I. István Gimn., IV. o. t.)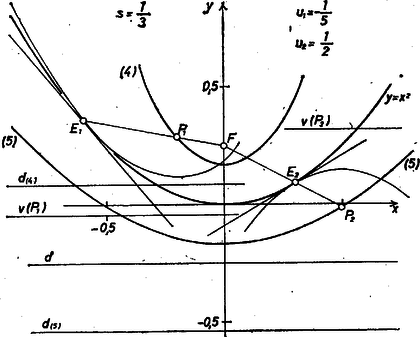

5. ábra

Az 5. ábra az

s = 1 / 3

értékhez tartozó parabolapárt tünteti fel (vastagon rajzolva), továbbá az első parabolán a

- 1 / 5

abszcisszájú

P_{1}

, a másodikon az

1 / 2

abszcisszájú

P_{2}

ponthoz tartozó kívánt

v (P_{1})

v (P_{2})

vezéregyenest, végül az ezekből kapott, az

y = x^{2}

parabolát érintő parabolákat (vékonyan rajzolva).