Kezdőlap


Feladat:	F.1770	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1971/október, 56 - 58. oldal		PDF \| MathML
Témakör(ök):	Súlypont, Parabola egyenlete, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1971/április: F.1770

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bármely két parabola hasonló egymáshoz, ezért elég az $y = x^{2}$ egyenletű $p$ parabolát tekintenünk. Legyen $A$ , $B$ , $C$ abszcisszája rendre $a$ , $b$ , $c$ , ekkor ordinátáik $a^{2}$ , $b^{2}$ ill. $c^{2}$ és $(a - b) (b - c) (c - a) \neq 0$ elegendő feltétele annak, hogy $A$ , $B$ és $C$ különböző pontok legyenek, mert $p$ -nek minden, a tengelyével párhuzamos egyenesen pontosan egy pontja van.
$p$ tetszőleges $(x_{1}, x_{1}^{2})$ pontjában az érintő iránytangense az $(x^{2})' = 2 x$ derivált értéke e helyen, azaz $2 x_{1}$ , a normálisé pedig ‐ $1 / (2 x_{1})$ , (hacsak $x_{1} \neq 0$ ), így a normális egyenlete az egy előírt ponton átmenő, előírt irányú egyenes egyenlettípusa alapján

\begin{matrix} y - x_{1}^{2} & = - \frac{1}{2 x_{1}} (x - x_{1}), rendezve \\ x & + 2 x_{1} y - 2 x_{1}^{3} - x_{1} = 0. & (1) \end{matrix}

Ha pedig

x_{1} = 0

, vagyis a pont éppen a

p

csúcsa, akkor a normális az

y

tengely, egyenlete

x = 0

, az átrendezett (1) alak már ezt is tartalmazza.

p

-nek bármely két különböző pontjához tartozó normálisa metszi egymást egyetlen pontban, mert iránytangenseik különbözők.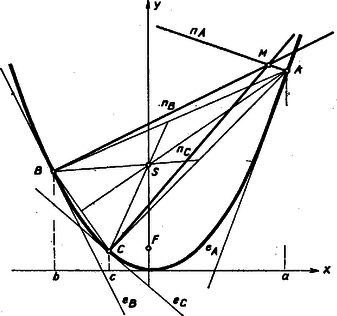

Annak feltételét keressük, hogy a kérdéses 3 normális,

n_{A}

n_{B}

n_{C}

közül az első kettőnek a metszéspontja egybeessék az első és a harmadik metszéspontjával. (1)-ben

x_{1}

helyére rendre

a

-t, ill.

b

-t írva

\begin{matrix} n_{A} egyenlete x + 2 a y - 2 a^{3} - a = 0, \\ n_{B} egyenlete x + 2 b y - 2 b^{3} - b = 0, \end{matrix}

innen

M

metszéspontjuk koordinátái, figyelembe véve, hogy

b \neq a

\begin{matrix} y_{M} = a^{2} + a b + b^{2} + \frac{1}{2}, x_{M} = - 2 a b (a + b) . \end{matrix}

Ebből

n_{A}

és

n_{C}

-nek

M'

metszéspontja koordinátáit úgy kapjuk, hogy

b

helyére

c

-t írunk:

\begin{matrix} y_{M'} = a^{2} + a c + c^{2} + \frac{1}{2}, x_{M'} = - 2 a c (a + c) . \end{matrix}

A 3 normális akkor megy át egy ponton, ha

M'

azonos

M

-mel, hiszen ekkor ez a pont rajta van

n_{B}

-n is,

n_{C}

-n is, tehát egyben

n_{B}

és

n_{C}

metszéspontja.

M'

akkor és csakis akkor esik egybe

M

-mel, ha teljesül

y_{M'} = y_{M}

, hiszen egyetlen normális sem párhuzamos az

x

tengellyel, bármelyik normálison az ordináta egyértelműen meghatározza az abszcisszát, tehát a mondott feltétel maga után vonja

x_{M'}

, és

x_{M}

egyenlőségét is. Mármost

y_{M} = y_{M'}

, ha

y_{M} - y_{M'} = a (b - c) + b^{2} - c^{2} = (b - c) (a + b + c) = 0

, és ez, mivel

(b - c) \neq 0

, akkor és csak akkor teljesül, ha

\begin{matrix} a + b + c = 0. \end{matrix}

(2)

Ez, mint ismeretes, azt jelenti, hogy az

A B C

háromszög

S

súlypontja rajta legyen az

x = 0

egyenesen, az

y

tengelyen, ill. a koordináta-rendszertől elvonatkoztatva, hogy

S

p

szimmetriatengelyén legyen.

Megjegyzés. Miután felírtuk a normálisok egyenletét, megoldásunkat így is folytathatjuk: Annak a feltételét keressük, hogy az

\begin{matrix} x + 2 a y - 2 a^{3} - a = 0 \\ x + 2 b y - 2 b^{3} - b = 0 \\ x + 2 c y - 2 c^{3} - c = 0 \end{matrix}

egyenletű egyeneseknek legyen közös pontja, vagyis legyen olyan

(x_{0}, y_{0})

számpár, melyre az

\begin{matrix} x_{0} + 2 z y_{0} - 2 z^{3} - z = 0 \end{matrix}

(3)

harmadfokú egyenletnek az

a

b

c

(különböző ) számok a gyökei. A gyökök és együtthatók közti összefüggések¹ szerint az

\begin{matrix} A z^{3} + B z^{2} + C z + D = 0 \end{matrix}

harmadfokú egyenlet (melyben

A \neq 0)

gyökeinek összege

- \frac{B}{A}

, így

a

b

c

csak akkor lehet (3) gyöke, ha

\begin{matrix} a + b + c = 0, \end{matrix}

hiszen (3)-ban

z^{2}

nem szerepel. Ez a feltétel tehát szükséges ahhoz, hogy a három normális egy ponton menjen át.
Megmutatjuk, hogy a kapott feltétel elégséges is. Valóban, a gyökök és együtthatók összefüggése szerint

a

b

c

akkor és csakis akkor gyöke a

\begin{matrix} 2 z^{3} + B z^{2} + C z + D = 0 \end{matrix}

egyenletnek, ha

\begin{matrix} B = 2 (a + b + c), C = - 2 (a b + b c + c a), D = 2 a b c . \end{matrix}

Így, ha

a + b + c = 0

, akkor

\begin{matrix} x_{0} = D = 2 a b c, y_{0} = \frac{C + 1}{2} = \frac{1}{2} - (a b + b c + c a) \end{matrix}

mellett

a

b

c

gyöke a (3) egyenletnek, vagyis a három normális átmegy az

(x_{0}, y_{0})

ponton.

¹Lásd pl. Hack Frigyes ‐ Kugler Sándorné: Függvénytáblázatok. Matematikai és fizikai összefüggések. Tankönyvkiadó, Budapest, 1968. 66. old. 25.33. képletcsoport.