Cím:	Megoldásvázlatok a 2005/4. sz. II. középszintű gyakorló feladataihoz
Szerző(k):	Kántor Sándorné Varga Tünde
Füzet:	2005/áprilisi melléklet, 70 - 74. oldal	PDF  |  MathML
Témakör(ök):	Ábrázoló geometria
Hivatkozás(ok):	2005/extra1: Középszintű gyakorló feladatsor II.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. A válasz: (B). I. $x^x+x^x=2x^x$. II. $x^{2x}={\left(x^x\right)}^2\ne 2x^x$. III. ${\left(2x\right)}^x=2^x{x}^x\ne 2x^x$. IV. ${\left(2x\right)}^{2x}=2^{2x}\cdot x^{2x}\ne 2x^x$.   2. A válasz: (D). $\begin{array}{c}{\displaystyle {\left(\frac{3}{5}\right)}^{2005}\cdot \frac{5^{2006}+5^{4012}}{3^{2006}+{15}^{2006}}=\frac{3^{2005}\cdot 5^{2006}\left(1+5^{2006}\right)}{5^{2005}\cdot 3^{2006}\left(1+5^{2006}\right)}=\frac{5}{3}\mathrm{.}}\end{array}$   3. Anna 4 napos, Béla 10 napos ciklusban dolgozik, így 4 és 10 legkisebb közös többszörösét kell kiszámolni, tehát 20 naposak az egyes ciklusok. Egy cikluson belül 2 szabadnap közös. A 120 nap alatt 6 ilyen ciklus van, így 12-szer lesz közös a szabadnapjuk.   4. $\overrightarrow{AD}=\left(8;3\right)$, $\overrightarrow{BC}=\left(12;4\mathrm{,}5\right)$, így $\overrightarrow{BC}=\frac{3}{2}\overrightarrow{AD}$, ezért a négyszög trapéz és nem paralelogramma.   5. A válasz (A). $\begin{array}{c}{\displaystyle \frac{32000\cdot 1\mathrm{,}05+8000\cdot 1\mathrm{,}1}{40000}=\frac{42\mathrm{,}4}{40}=1\mathrm{,}06.}\end{array}$ Az emelkedés 6%-os volt.   6. $a)$ $A=\left\{0;1;2\right\}$, $B=\left\{-2;2\right\}$, $C=\left\{2;3;5\right\}$. $b)$ $A\cap B\cap C=\left\{2\right\}$. $c)$ $B$ nem részhalmaza az $A$-nak, mert $-2\notin A$.   7. $a)$ $x^2-1\ge 0$, $x^2\ge 1$, tehát $x\ge 1$ vagy $x\le -1$. $b)$ $1-x>0$, $x<1$.   8. $4^x-2^{x+1}=3$, amiből ekvivalens átalakítással $\begin{array}{c}{\displaystyle 2^{2x}-2\cdot 2^x-3=0.}\end{array}$ $2^x=a$ helyettesítéssel az $a^2-2a-3=0$ másodfokú egyenletet kapjuk, amelynek gyökei: $a_1=3$, $a_2=-1$. Mivel $2^x>0$, azért csak az $a_1=2^x=3$ esetén kapunk megoldást: $\begin{array}{c}{\displaystyle x=\frac{\text{lg}3}{\text{lg}2}=\text{log}{}_{2}3.}\end{array}$ A kapott gyök kielégíti az eredeti egyenletet.   9. Az egy napi gyógyszer ára: $\frac{1470\text{Ft}}{14}=105$ Ft. Az egy napi gyógyszerfogyasztás: a zöld kapszulából 3 darab, fehér kapszulából két darab. Ha egy zöld kapszula ára $x$ Ft, akkor egy fehér kapszula ára $\left(x-10\right)$ Ft. A napi fogyasztás ára: $\begin{array}{c}{\displaystyle 3x+2\left(x-10\right)=\mathrm{105,}}\end{array}$ amiből $x=25$ és $x-10=15$. Így egy darab zöld kapszula ára 25 Ft, egy darab fehér kapszula ára 15 Ft.   10. A válasz: (B). Az ábráról leolvashatjuk a grafikonnak a koordináta-tengelyekkel való metszéspontjait. $f\left(0\right)=2$, ezért $d=2$; $f\left(-1\right)=0$, ezért $0=-a+b-c+2$; $f\left(1\right)=0$, ezért $0=a+b+c+2$. Így $2b+4=0$, tehát $b=-2$.   11. Legyen a kúp és a gömb közös sugarának nagysága: $r$.     A gömb térfogata: $V_{\text{gömb}}=\frac{4r^3\pi }{3}$, a kúp térfogata: $\begin{array}{c}{\displaystyle V_{\text{kúp}}=\frac{r^2\pi \cdot m}{3}\mathrm{.}}\end{array}$ A feltételek miatt: $\begin{array}{c}{\displaystyle \frac{3}{4}\cdot \frac{4r^3\pi }{3}=\frac{r^2\pi \cdot m}{3}\mathrm{,}}\end{array}$ amiből $m=3r$.   Így a tölcsérkúp magassága és a fagylaltgömb sugara hosszának az aránya $3:1$.   12. A válasz: (B). Ábrát készítünk. 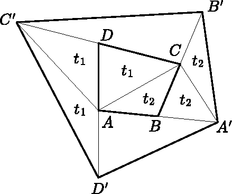    Az $ABCD$ négyszöget az $AC$, illetve a $BD$ átlója két-két háromszögre bontja. Nyilvánvaló, hogy ezek területének összege megegyezik az $ABCD$ négyszög területével. Felhasználjuk, hogy egy háromszöget a súlyvonala két egyenlő területű háromszögre bont: ${\displaystyle \begin{array}{c}\hfill {\displaystyle T_{A\text{'}B\text{'}C\text{'}D\text{'}}=T_{ABCD}+T_{DC\text{'}D\text{'}}+T_{B\text{'}BA\text{'}}+}\hfill \\ \hfill {\displaystyle +T_{C\text{'}CB\text{'}}+T_{D\text{'}A\text{'}A}=5T_{ABCD}\mathrm{.}}\hfill \end{array}}$ A keresett arány: $5:1$.   II./A rész   13. $a)$ Az $x\mapsto \text{cos}2x$ függvény grafikonját az $x\mapsto \text{cos}x$ függvény transzformációjának a segítségével készítjük el. 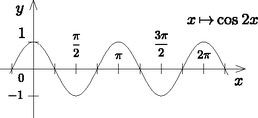    Helyi maximuma van a függvénynek az $x=k\cdot \pi$, $k\in \text{Z}$ helyeken és értéke 1. Helyi minimuma van a függvénynek az $x=\frac{\pi }{2}+k\cdot \pi$, $k\in \text{Z}$ helyeken és értéke $-1$. $b)$ Felhasználjuk, hogy $\text{ctg}x=\frac{\text{cos}x}{\text{sin}x}$. $\text{cos}{}^{2}x-8\text{sin}{}^{4}x=\text{sin}{}^{2}x$, amiből $8\text{sin}{}^{4}x+2\text{sin}{}^{2}x-1=0$, $\begin{array}{c}{\displaystyle \text{sin}{}^{2}x=\frac{-2\pm 6}{16}\mathrm{,}\text{sin}{}^2{x}_1=\frac{1}{4}\mathrm{,}\text{sin}{}^2{x}_2=-\frac{1}{2}\mathrm{.}}\end{array}$ Ez utóbbi nem megfelelő, mivel $\text{sin}{}^{2}x\ge 0$, tehát $\text{sin}x=\frac{1}{2}$ vagy $\text{sin}x=-\frac{1}{2}$, amiből az egyenlet megoldásai: $x=\pm \frac{\pi }{6}+k\pi$, $k\in \text{Z}$. Mindegyik gyök kielégíti az eredeti egyenletet.   14. $a)$ (I) $x-2y=3$, (II) $3x-y=4$ egyenletrendszert megoldjuk, pl. a behelyettesítő módszerrel. (I)-ből $x=2y+3$, amit (II)-be visszahelyettesítünk. Így megkapjuk, hogy $y=-1$, $x=1$, tehát az $M$ metszéspont koordinátái: $\left(1;-1\right)$. $b)$ A $h$ egyenes illeszkedik az $M\left(1;-1\right)$ pontra. A $g$ egyenes normálvektora: ${\text{n}}_g\left(2;-3\right)$. A $h$ egyenes normálvektora pl.: ${\text{n}}_h\left(3;2\right)$.     A keresett $h$ egyenes egyenlete: $\begin{array}{c}{\displaystyle 3x+2y=3-2=\mathrm{1,}}\end{array}$ vagy más formában $\begin{array}{c}{\displaystyle y=-\frac{3}{2}\cdot x+\frac{1}{2}\mathrm{.}}\end{array}$ $c)$ A $h$ egyenes az $A\left(0;\frac{1}{2}\right)$ pontban metszi az $y$ tengelyt, a $B\left(\frac{1}{3};0\right)$ pontban metszi az $x$ tengelyt.   15. Legyen $d\left(BC\right)=2a$. Jelöljük a $BC$ oldal felezőpontját $F$-fel és legyen $BFA\sphericalangle =\delta$. Ekkor $\begin{array}{c}{\displaystyle AFC\sphericalangle ={180}^{\circ }-\delta \text{és}\text{cos}\left({180}^{\circ }-\delta \right)=-\text{cos}\delta \mathrm{.}}\end{array}$ Írjuk fel a koszinusz tételt az $ABF$ és az $AFC$ háromszögekre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a^2+4a^2-4a^2\text{cos}\delta }& {\displaystyle =1}\hfill \\ \hfill {\displaystyle a^2+4a^2+4a^2\text{cos}\delta }& {\displaystyle =\mathrm{4,}}\hfill \end{array}}$ amiből $10a^2=5$, $a=\frac{\sqrt[]{2}}{2}$. Így $d\left(BC\right)=2a=\sqrt[]{2}$ (cm).     Közelítő értékkel (1 tizedes jegy pontosságig, az adatok pontosságának megfelelően) $d\left(BC\right)\approx 1\mathrm{,}4$ cm.   II./B rész   16. Ha a 2-es számot tartalmazó cédulát háromszor húztuk ki és a számok összege 6, akkor a feljegyzésünk: $\left(2;2;2\right)$. Tehát a kedvező esetek száma: 1. Az összes eset, amikor a számjegyek összege 6, a következő: $\begin{array}{c}{\displaystyle \left(1;2;3\right);\left(1;3;2\right);\left(2;3;1\right);\left(2;1;3\right);\left(3;1;2\right);\left(3;2;1\right);\left(2;2;2\right)\mathrm{.}}\end{array}$ Így összesen 7 eset van. A keresett valószínűség: $\frac{1}{7}$.   17. $a)$ $a_4$, $a_7$, $a_{10}$ is egy számtani sorozat három szonszédos tagja. Ha $a_7=x$, akkor $\begin{array}{c}{\displaystyle \left(x-3d\right)+x+\left(x+3d\right)=\mathrm{17,}}\end{array}$ amiből $a_7=\frac{17}{3}$. $b)$ $a_4\mathrm{,}{a}_5\mathrm{,}\text{...}\mathrm{,}{a}_9\mathrm{,}\text{...}\mathrm{,}{a}_{13}\mathrm{,}{a}_{14}$ tagok közül a mediánt (a középsőt), vagyis $a_9$-et $y$-nal jelölve és felhasználva a számtani sorozat definícióját kapjuk, hogy $\begin{array}{c}{\displaystyle \left(y-5d\right)+\left(y-4d\right)+\text{...}+\left(y-d\right)+y+\left(y+d\right)+\text{...}+\left(y+4d\right)+\left(y+5d\right)=\mathrm{77,}}\end{array}$ innen $y=a_9=7$. $c)$ Mivel $a_9-a_7=2d$, azért $d=\frac{2}{3}$. $d)$ $a_7=a_1+6d$, amiből $a_1=\frac{5}{3}$. $e)$ $a_k=a_1+\left(k-1\right)d$, $13=\frac{5}{3}+\left(k-1\right)\cdot \frac{2}{3}$, amiből $k=18$, tehát $a_{18}=13$.   18. A fácánok száma: 2001-ben 39, 2002-ben 60, 2003-ban $x$, 2004-ben 123. $a)$ A feltétel szerint: $x-39=60\cdot k$, ahol $k$ az arányossági tényező és $123-60=k\cdot x$. Innen $\begin{array}{c}{\displaystyle k=\frac{63}{x}\mathrm{,}x-39=60\cdot \frac{63}{x}\mathrm{,}{x}^2-39x-3780=\mathrm{0,}{x}_1=\mathrm{84,}{x}_2=-45<\mathrm{0,}}\end{array}$ így $x_2$ nem felel meg a feladat feltételeinek. A fácánok létszáma 2003-ban 84 volt. $b)$ Az oszlopdiagram: