Kezdőlap


Feladat:	5016. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Vaszary Tamás
Füzet:	2018/szeptember, 375 - 376. oldal		PDF \| MathML
Témakör(ök):	Feladat, Erők forgatónyomatéka, Tapadó súrlódás
Hivatkozás(ok):	Feladatok: 2018/március: 5016. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a lassan (gyorsulásmentesen) mozgatott rúd azon állapotát, amikor $α$ szöget zár be a vízszintessel $(0 \leq α \leq 90^{\circ})$ . Az $ℓ$ hosszú rúdra négyféle erő hat: a rúd megemelt végénél a rúdra merőleges $F$ erő, a rúd felezőpontjánál függőlegesen lefelé ható $G$ nehézségi erő, a rúd alsó végénél pedig a függőlegesen felfelé ható $N$ nyomóerő és a vízszintes $S$ súrlódási erő (lásd az ábrát).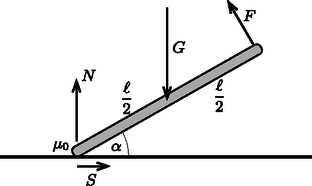

Az erők és a forgatónyomatékok egyensúlyának feltétele:

\begin{matrix} F sin α & = S, & (1) \\ F cos α + N & = G, & (2) \\ F ℓ & = G \frac{ℓ}{2} cos α . & (3) \end{matrix}

Ezekből megkaphatjuk, hogy

\begin{matrix} F & = \frac{G}{2} cos α, & (4) \\ S & = \frac{G}{2} sin α cos α, & (5) \end{matrix}

\begin{matrix} N = (1 - \frac{cos^{2} α}{2}) G . \end{matrix}

(6)

Annak a feltétele, hogy a rúd az

α

szögű helyzetben nem csúszik meg:

\begin{matrix} μ_{0} \geq \frac{S (α)}{N (α)} = \frac{sin α cos α}{2 - cos^{2} α} \equiv f (α), \end{matrix}

(7)

ahol

μ_{0}

a rúd és az asztallap közötti tapadó súrlódási együttható.
A rúd akkor állítható fel a megadott módon, ha a (7) egyenlőtlenség tetszőleges

0 \leq α \leq 90^{\circ}

szögnél teljesül, vagyis

μ_{0}

nem kisebb, mint az

f (α)

függvény maximális értéke.

f (α)

legnagyobb értékét numerikus módszerekkel (táblázat készítésével), differenciálszámítással vagy a WolframAlpha program felhasználásával kaphatjuk meg, de elemi módszerekkel is célhoz érhetünk. Ha

sin α

-t és

cos α

-t kifejezzük

tg α

-val, a vizsgálandó függvény reciprokára a következő kifejezést kapjuk:

\begin{matrix} \frac{1}{f (α)} = \frac{1}{tg α} + 2 tg α . \end{matrix}

Alkalmazva a számtani-mértani középre vonatkozó egyenlőtlenséget:

\begin{matrix} \frac{1}{f (α)} \geq 2 \sqrt[]{\frac{1}{tg α} \cdot 2 tg α} = \sqrt[]{8} . \end{matrix}

Ezek szerint

f (α)

legnagyobb értéke, vagyis a csúszásmentes emeléshez szükséges legkisebb súrlódási együttható nagysága:

\begin{matrix} μ_{0}^{kritikus} = \frac{1}{\sqrt[]{8}} \approx 0, 35. \end{matrix}

Vaszary Tamás (Győr, Kazinczy F. Gimn., 10. évf.)
dolgozata alapján