Kezdőlap


Feladat:	B.4865	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke Csongor , Borbényi Márton , Csahók Tímea , Daróczi Sándor , Gáspár Attila , Imolay András , Kerekes Anna , Kővári Péter Viktor , Németh Balázs , Szabó Kristóf , Tóth Viktor
Füzet:	2018/április, 213 - 214. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Trigonometriai azonosságok, Trigonometrikus egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2017/március: B.4865

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit, a $C$ -ből induló szögfelező hossza legyen $d$ , a háromszög belső szögei $α$ , $β$ és $γ$ . Írjuk fel $A B C ▵$ területét kétféleképpen: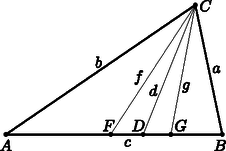

\begin{matrix} \frac{a b sin γ}{2} & = T_{A B C} = T_{A D C} + T_{B C D} = \\ = \frac{d b sin \frac{γ}{2}}{2} + \frac{a d sin \frac{γ}{2}}{2} . \end{matrix}

Innen, felhasználva hogy

sin γ = 2 sin \frac{γ}{2} cos \frac{γ}{2}

, kapjuk:

\begin{matrix} \frac{2 a b}{a + b} = \frac{2}{\frac{1}{a} + \frac{1}{b}} = \frac{d}{cos \frac{γ}{2}} . \end{matrix}

A kitűzöttnél erősebb

\begin{matrix} {max}_{}^{} {f, g} < \frac{2}{\frac{1}{a} + \frac{1}{b}} = \frac{d}{cos \frac{γ}{2}} \end{matrix}

(1)

állítást fogjuk igazolni. Az

F D C

háromszögben

F ∢ = α + γ / 3

és

D ∢ = β + γ / 2

, így a szinusz-tétel szerint

\begin{matrix} \frac{f}{d} = \frac{sin (β + \frac{γ}{2})}{sin (α + \frac{γ}{3})} = \frac{sin (α + \frac{γ}{2})}{sin (α + \frac{γ}{3})} . \end{matrix}

Megmutatjuk, hogy ha

0 < α, γ < π / 2

és

α + γ \geq π / 2

, akkor

\begin{matrix} \frac{sin (α + \frac{γ}{2}) cos \frac{γ}{2}}{sin (α + \frac{γ}{3})} < 1. \end{matrix}

(2)

Ebből, mivel

f

és

g

szerepe szimmetrikus, következik (1). Először tegyük fel, hogy

α + γ = π / 2

. Ekkor

\begin{matrix} \frac{sin (α + \frac{γ}{2}) cos \frac{γ}{2}}{sin (α + \frac{γ}{3})} & = \frac{sin (\frac{π}{2} - \frac{γ}{2}) cos \frac{γ}{2}}{sin (\frac{π}{2} - \frac{2 γ}{3})} = \frac{cos^{2} \frac{γ}{2}}{cos \frac{2 γ}{3}} = \\ = \frac{1 + cos γ}{2 cos \frac{2 γ}{3}} = \frac{1 + 4 cos^{3} \frac{γ}{3} - 3 cos \frac{γ}{3}}{4 cos^{2} \frac{γ}{3} - 2} . \end{matrix}

Mivel

0 < γ / 3 < π / 6

, így

\sqrt[]{3} / 2 < cos γ / 3 < 1

. Az

x : = cos γ / 3

jelölést bevezetve ez a bizonyítandó állítás:

\begin{matrix} \frac{4 x^{3} - 3 x + 1}{4 x^{2} - 2} < 1 \Leftrightarrow 4 x^{3} - 4 x^{2} - 3 x + 3 < 0 \Leftrightarrow (x - 1) (4 x^{2} - 3) < 0. \end{matrix}

Ez pedig nyilvánvalóan teljesül, mert

x - 1 < 0

és

4 x^{2} - 3 > 0

, ezért

α + γ = π / 2

esetén (2)-t beláttuk.
Most rögzítsük

γ

-t, és legyen

\begin{matrix} f (α) = \frac{sin (α + \frac{γ}{2}) cos \frac{γ}{2}}{sin (α + \frac{γ}{3})} . \end{matrix}

Megmutatjuk, hogy

f

[π / 2 - γ, π / 2]

intervallumon monoton csökken. Ehhez deriváljuk

f

-et:

\begin{matrix} f' (α) & = cos \frac{γ}{2} \cdot \frac{cos (α + \frac{γ}{2}) sin (α + \frac{γ}{3}) - sin (α + \frac{γ}{2}) cos (α + \frac{γ}{3})}{sin^{2} (α + \frac{γ}{3})} = \\ = \frac{cos \frac{γ}{2} sin \frac{- γ}{6}}{sin^{2} (α + \frac{γ}{3})} . \end{matrix}

A derivált triviálisan negatív, így

f

valóban monoton csökkenő. Ebből és az

α + γ = π / 2

speciális esetből (2) és így az állítás is következik.

Megjegyzések: 1. A (2) egyenlőtlenséget deriválás nélkül, trigonometrikus azonosságok ügyes alkalmazásával is igazolhatjuk. Érdemes azonban a bemutatott módszert észben tartani, amikor egyenlőtlenséget akarunk bizonyítani. Ha a derivált előjele triviálisan látszik, mint esetünkben is, akkor biztosan megkönnyíti a számolást.
2. Honlapunkon található a feladatra két elemi megoldás, amelyek nem használnak differenciálszámítást.