Kezdőlap


Feladat:	B.4863	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gáspár Attila
Füzet:	2018/február, 90. oldal		PDF \| MathML
Témakör(ök):	Feladat, Tengelyes tükrözés, Síkgeometriai bizonyítások, Pont körüli forgatás
Hivatkozás(ok):	Feladatok: 2017/március: B.4863

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $O$ az $A B C ▵$ körülírt körének középpontja, és használjuk az ábra jelöléseit. A kerületi- és középponti szögek tétele miatt $A D C ∢ = 2 A B C ∢ = A O C ∢$ , ezért az $A$ , $C$ , $D$ és $O$ pontok egy körre illeszkednek. Az $A D = D C$ esetben $D = O$ , az állítás triviális, ezért a továbbiakban az általánosság megszorítása nélkül feltesszük, hogy 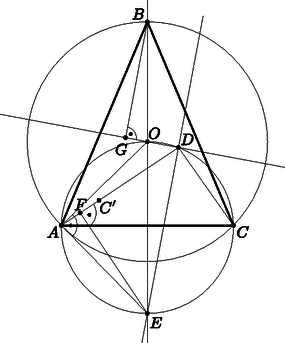$A D > D C$ .

A D C ∢

szögfelezője az

A D C

kört az

O

-val átellenes

E

pontban metszi, ami felezi az

A C

ívet. A

C

pont

D E

-re vonatkozó

C'

tükörképe illeszkedik

A D

-re. Így

A E = C E = C' E

, s ezért az

A C'

szakasz

F

felezőpontjára

E F C' ∢ = 90^{\circ}

teljesül. Innen egyrészt a felezés miatt

\begin{matrix} D F = \frac{D C' + D A}{2} = \frac{D C + D A}{2}, \end{matrix}

másrészt definíció szerint

D F = D E \cdot cos (F D E ∢)

.
Mivel

O E

átmérő, a Thalész-tétel miatt

O D E ∢ = O A E ∢ = 90^{\circ}

. A külső és a belső szögfelezők merőlegesek egymásra, így

O D

éppen a

D

-nél lévő külső szögfelező. Legyen

G

B

merőleges vetülete

O D

-n. A szimmetria miatt

B

O

és

E

kollineárisak, így az

O D E ▵

és a

O G B ▵

szögei páronként megegyeznek, ezért a háromszögek hasonlóak. Ezt kihasználva

\begin{matrix} B G & = \frac{B O}{O E} \cdot D E = \frac{A O}{O E} \cdot D E = cos (A O E ∢) \cdot D E = cos (F D E ∢) \cdot D E = \\ = \frac{D C + D A}{2}, \end{matrix}

amivel az állítást beláttuk.

Gáspár Attila (Miskolc, Földes Ferenc Gimn., 11. évf.)