Feladat: B.4843 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 2017/december, 539 - 541. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai bizonyítások, Tengelyes tükrözés, Szögfelező egyenes
Hivatkozás(ok):Feladatok: 2017/január: B.4843

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Megoldás. A feladat megoldása három jól elkülöníthető, önmagában is figyelemre érdemes lépésre bontható. Ezeket külön segédállításokként fogalmazzuk meg, ahol lehetséges, többféle indoklást is mutatunk.
 
1. segédállítás. Ha az ABC háromszög AC és BC oldalain felvett K és L pontokra AK=BL, akkor az AB és KL szakaszok felezőpontjain átmenő egyenes párhuzamos az ACB∢ szögfelezőjével.
 
1. bizonyítás (vektorokkal, Győrffy Ágoston (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.) megoldása). Az AB szakasz felezőpontja legyen F, a KL szakaszé pedig M. A vektorok összeadásának definíciója szerint MF→=MK→+KA→+AF→ és MF→=ML→+LB→+BF→. Ebből, felhasználva, hogy MK→=-ML→ és AF→=-BF→, kapjuk, hogy 2MF→=KA→+LB→. A feltétel szerint |KA→|=|LB→|, így a vektorösszeadást paralelogramma-módszerrel végezve egy rombuszt kapunk, aminek 2MF→ átlója valóban felezi a KA→ és LB→ vektorok szögét, ahogy állítottuk (1. ábra).  □


 

1. ábra
 

 
2. bizonyítás (elemi szögszámítással, Daróczi Sándor (Nyíregyháza, Krúdy Gyula Gimn., 11. évf.) megoldása). Használjuk a 2. ábra jelöléseit. Tükrözzük az ABLK négyszöget és az F pontot középpontosan az M-re, így kapjuk az A', B', L' és K', valamint F' pontokat. A tükrözés miatt ABA'B' paralelogramma, aminek FF' középvonala, így AFF'B' is paralelogramma; valamint KB'A'∢=β. Továbbá AK=BL=B'L' miatt a B'AK▵ egyenlőszárú, így B'AK∢=KB'A∢=δ. Mivel α+β<180∘, K az ABA'B' paralelogramma belső pontja, és a 2. ábra helyes. Az ábráról leolvasható, hogy α+β+2δ egyenesszög, mivel egy paralelogramma egy szárán fekvő két szög összege. Ebből következik, hogy az ABC▵-ben C∢=2δ, amiből CG szögfelezése miatt GCB∢=δ. A tükrözés miatt B'K∥BL=BC, amiből GCB∢=AB'K∢ miatt CG∥B'A∥F'F, amivel az állítást beláttuk.  □


 

2. ábra
 

 
Megjegyzés. Az első, vektorokat használó megoldásból kitűnik, hogy nem szükséges feltennünk, hogy K és L a háromszög oldalainak egy-egy pontja, elegendő, hogy az oldalegyeneseken vannak, és AK=BL. Azonban attól függően, hogy K és L melyik A-hoz illetve B-hez tartozó félegyenesre kerül, változhat, hogy a C∢ melyik szögfelezőjével lesz párhuzamos az FM egyenes.

 
2. segédállítás. Az ABC háromszög AB oldalának felezőpontja legyen F, és F-en keresztül húzzuk meg a BCA∢ szög (belső) szögfelezőjével párhuzamos e egyenest. Ekkor az e egyenes felezi az ABC▵ kerületét.
 
1. bizonyítás (az 1. segédállításból közvetlenül). Az a=b eset triviális, így az általánosság megszorítása nélkül feltehetjük, hogy a>b, és használjuk a 3. ábra jelöléseit. Legyen C' a BC oldal azon pontja, amelyre BC'=AC, továbbá legyen P a CC' szakasz felezőpontja. Alkalmazzuk az 1. segédállítást a K=C és L=C' pontokra. Kapjuk, hogy a PF egyenes párhuzamos a CG szögfelezővel, azaz PF=e. Az AF=FB, AC=BC' és C'P=PC nyilvánvaló egyenlőségekből adódik az állítás.  □


 

3. ábra
 

 
2. bizonyítás (szögfelező-tételből, Győrffy Ágoston (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 10. évf.) megoldása). Ismét feltesszük, hogy a>b. A szögfelező-tétel szerint egy háromszög szögfelezője a szemközti oldalt a szomszédos oldalak arányában osztja, azaz AG/GB=b/a. Innen arányos osztással GB=ca/(a+b) azonnal adódik. Az ABC∢-ben felírhatjuk a párhuzamos szelők tételét a CG szögfelezőre és az e egyenesre ‐ a P pontot most e∩BC-ként definiáljuk:
BFBG=BPBC.
Innen
BP=c/2ca/(a+b)⋅a=a+b2,
és végül BF+BP=c/2+(a+b)/2=k/2 valóban a kerület fele, ahogy állítottuk.  □
 
3. bizonyítás (Menelaosz-tételből). Továbbra is feltesszük, hogy a>b. Messe e a BC-t P-ben, az AC-t pedig Q-ban a 3. ábra szerint. Mivel e párhuzamos a CG szögfelezővel, PQC∢=GCA∢=GCB∢=CPQ∢, azaz PQC▵ egyenlőszárú. Írjuk fel a Menelaosz-tételt az ABC▵-re és az e egyenesre:
AF⋅BP⋅CQ=BF⋅AQ⋅CP.
Az AF=BF és PC=CQ egyszerűsítések után AQ=BP adódik, amiből PC=CQ=x jelöléssel a-x=b+x, és x=(a-b)/2 következik. Így FA+AC+CP=c/2+b+(a-b)/2=k/2, ahogy állítottuk.  □
 
3. segédállítás. Az ABC háromszög AC, illetve BC oldalaihoz írt köröknek az oldalakon levő érintési pontjai rendre K és L. Ekkor AK=BL.
 
Bizonyítás. Az állítás jól ismert, a teljesség kedvéért közöljük a bizonyítását. A szokásos jelöléseket használjuk, s=(a+b+c)/2 az ABC▵ félkerülete. Az AC oldalhoz írt kör érintési pontjai az AB és BC oldalegyeneseken legyenek rendre H és G. Mivel külső pontból körhöz húzott érintőszakaszok egyenlőek, azért CG=CK, AH=AK és BG=BH. Ezeket felhasználva
BH+BG=BA+AH+BC+CG=BA+AK+BC+CK=a+b+c=2s,
így BH=s, és AK=AH=BH-BA=s-c adódik. Hasonló számolással BL=s-c, amiből az állítás következik.  □


 

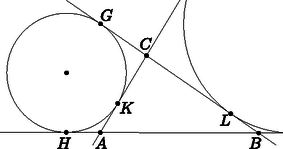4. ábra
 

 
A B. 4843. feladat megoldása. A három segédállításból a feladat állítása azonnal következik. A 3. segédállítás szerint AK=BL. Ezután az 1. segédállítás miatt a KL és AB szakaszok felezőpontjain átmenő egyenes párhuzamos az ACB∢ szögfelezőjével, végül a 2. segédállítás szerint felezi a háromszög kerületét.  □