Feladat:	B.4737	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2017/december, 537. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai számítások trigonometria nélkül, Háromszög nevezetes körei, Párhuzamos szelőszakaszok tétele
Hivatkozás(ok):	Feladatok: 2015/október: B.4737

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.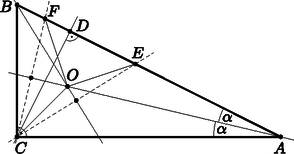   Megoldás. Először megmutatjuk, hogy a két kör középpontja egybeesik. Jelölje $2\alpha$ az $ABC$ háromszög $A$-nál lévő szögét, $O$ pedig a háromszög szögfelezőinek metszéspontját. Mivel a merőleges szárú hegyesszögek egyenlőek, ezért $CAD\sphericalangle =BCD\sphericalangle =2\alpha$ (1. ábra), tehát $\begin{array}{c}{\displaystyle FCA\sphericalangle =FCD\sphericalangle +DCA\sphericalangle =\alpha +\left({90}^{\circ }-2\alpha \right)={90}^{\circ }-\alpha \mathrm{.}}\end{array}$ Az $AFC$ háromszögben a szögek összege ${180}^{\circ }$, tehát $\begin{array}{c}{\displaystyle AFC\sphericalangle ={180}^{\circ }-\left(FCA\sphericalangle +CAF\sphericalangle \right)={90}^{\circ }-\alpha \mathrm{.}}\end{array}$ Ezért az $AFC$ háromszög egyenlőszárú, amiből következik, hogy szárszögének szögfelezője merőleges az alapjára. Tehát $CF$ szakaszfelező merőlegese az $AO$ egyenes. Ugyanígy kapjuk, hogy $CE$ szakaszfelező merőlegese pedig a $BO$ egyenes. Mivel két oldalfelező merőleges metszéspontja meghatározza a $CEF$ háromszög körülírt körének középpontját, ezért az egybeesik $O$-val.   1. ábra   Jelölje $P$, illetve $Q$ az $ABC$ háromszög beírt körének a befogókon lévő érintési pontjait (2. ábra). Mivel bármely külső pontból egy körhöz húzott két érintőszakasz hossza egyenlő, ezért $CP=CQ$. Nyilván teljesül $OP=OQ$ is, tehát a $CPOQ$ négyszög deltoid. Kör érintője merőleges az érintési pontba húzott sugárra, továbbá $PCQ\sphericalangle ={90}^{\circ }$, ezért a deltoidnak van három derékszöge, tehát téglalap is. Ha viszont egy deltoid téglalap, akkor az négyzet. 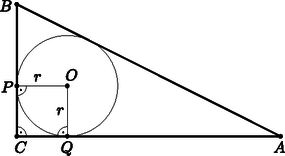  2. ábra   A két kör sugarainak keresett aránya tehát megegyezik a $CPOQ$ négyzet $OP$ oldalának és $OC$ átlójának arányával, azaz $\frac{1}{\sqrt[]{2}}=\frac{\sqrt[]{2}}{2}$.