Feladat:	B.4838	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Döbröntei Dávid Bence
Füzet:	2017/május, 278 - 279. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Térgeometriai bizonyítások, Egyéb poliéderek, Térbeli szimmetrikus alakzatok
Hivatkozás(ok):	Feladatok: 2016/december: B.4838

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Felhasználjuk a következő ismert tételt: bármely konvex poliédernek van háromszög lapja, vagy olyan csúcsa, amelyre pontosan három él illeszkedik. (Lásd például: Sklarszkij‐Csencov‐Jaglom: Válogatott fejezetek és tételek az elemi matematika köréből 3.; 44. feladat. (17. old.).) Így elegendő a következő két esetet vizsgálni. I. eset: Tegyük fel, hogy az $A$ csúcsra pontosan három él illeszkedik: $AB$, $AC$ és $AD$. Ekkor az $A$ csúcsra illeszkedő három lapsík $\langle ABC\rangle$, $\langle ABD\rangle$ és $\langle ACD\rangle$, ahol $\langle \cdot \rangle$ értelemszerűen a meghatározott síkot jelöli. A csúcsoknak az $O$ szimmetriaközéppontra vonatkozó tükörképei legyenek értelemszerűen $A\text{'}$, $B\text{'}$, $C\text{'}$ és $D\text{'}$. A feltétel szerint minden $A\text{'}$-től különböző csúcs, így $B\text{'}$, $C\text{'}$ és $D\text{'}$ is illeszkedik valamely $A$-ra illeszkedő lapsíkra. Világos, hogy $B$ és $B\text{'}$ nem illeszkedhet közös lapsíkra, ezért $B\text{'}\in \langle ACD\rangle$. A szimmetria miatt $\langle BD\text{'}A\text{'}C\text{'}\rangle$ is lapsík, vagyis $A\text{'}$ illeszkedik az $\langle ACD\rangle$-kal párhuzamos, $B$-re illeszkedő síkra. Hasonló megfontolással láthatjuk, hogy $A\text{'}$ illeszkedik az $\langle ABD\rangle$-kal párhuzamos, $C$-re illeszkedő síkra; valamint az $\langle ABC\rangle$-kal párhuzamos, $D$-re illeszkedő síkra is. Nyertük, hogy $A\text{'}$ éppen az $AB$, $AC$ és $AD$ élek által feszített paralelepipedon $A$-val szemközti csúcsa; $B\text{'}$, $C\text{'}$ és $D\text{'}$ a paralelepipedon további csúcsai. Azt is megmutattuk, hogy $\langle ABC\text{'}D\rangle$, $\langle ABD\text{'}C\rangle$ és $\langle ACB\text{'}D\rangle$, valamint ezek tükörképei: $\langle A\text{'}B\text{'}CD\text{'}\rangle$, $\langle A\text{'}B\text{'}DC\text{'}\rangle$ és $\langle A\text{'}C\text{'}BD\text{'}\rangle$ mind lapsíkok, így a poliéder szükségképpen az $ABCDA\text{'}B\text{'}C\text{'}D\text{'}$ paralelepipedon. II. eset: Tegyük fel, hogy, hogy $ABC$ egy háromszöglap. A szimmetriaközéppontot továbbra is jelölje $O$, az $ABC$ lap tükörképe legyen értelemszerűen $A\text{'}B\text{'}C\text{'}$. Első lépésként belátjuk, hogy az $A$, $B$, $C$, $A\text{'}$, $B\text{'}$ és $C\text{'}$ pontok éppen egy paralelepipedon lapközéppontjai. Legyen $\text{a}=\overrightarrow{OA}$, $\text{b}=\overrightarrow{OB}$ és $\text{c}=\overrightarrow{OC}$, ekkor a szimmetria miatt $\overrightarrow{OA\text{'}}=-\text{a}$, $\overrightarrow{OB\text{'}}=-\text{b}$ és $\overrightarrow{OC\text{'}}=-\text{c}$. Tekintsük azt a nyolc pontot, amelyekbe az $O$-ból mutató vektorok $\pm \text{a}\pm \text{b}\pm \text{c}$ alakúak. Ezek egy olyan paralelepipedon csúcsai, amelynek lapközéppontjai $A$, $B$, $C$, $A\text{'}$, $B\text{'}$ és $C\text{'}$. Ezt triviálisan teljesülő vektorazonosságok segítségével igazolhatjuk, a részletek végiggondolását az Olvasóra bízzuk. Megmutatjuk, hogy a poliéderünknek az $A$, $B$, $C$, $A\text{'}$, $B\text{'}$ és $C\text{'}$ pontoktól különböző csúcsa nem lehet. Tegyük fel, hogy $D$ egy további csúcs. A feltétel szerint $D$ az $A$, $B$, $C$, $A\text{'}$, $B\text{'}$ és $C\text{'}$ pontok mindegyikével illeszkedik egy közös lapra, vagyis a $DA$, $DB$, $DC$, $DA\text{'}$, $DB\text{'}$ és $DC\text{'}$ szakaszok mind a poliéder felszínén haladnak, továbbá $D$ szükségképpen szigorúan az $\langle ABC\rangle$ és $\langle A\text{'}B\text{'}C\text{'}\rangle$ síkok közé esik (hiszen a feltevés szerint $ABC$ és $A\text{'}B\text{'}C\text{'}$ háromszöglapok). Nyilvánvaló, hogy $D\notin \langle BCB\text{'}C\text{'}\rangle$, továbbá feltehető, hogy $D$ a $BCB\text{'}C\text{'}$ sík $A$-val átellenes oldalára esik (különben $A$ és $A\text{'}$ szerepét felcseréljük az indoklásban). A $DA$ szakasz a feltevés szerint a $BCB\text{'}C\text{'}$ paralelogrammát legfeljebb a határán metszheti, ezért a $D$ pontot vagy az $\langle ABC\text{'}\rangle$ vagy az $\langle ACB\text{'}\rangle$ elválasztja $O$-tól (ide értve azt is, hogy esetleg $D$ rajta van az $\langle ABC\text{'}\rangle$ vagy az $\langle ACB\text{'}\rangle$ síkok valamelyikén). Ismét az általánosság megszorítása nélkül feltehető, hogy $D$-t az $\langle ABC\text{'}\rangle$ választja el $O$-tól. Ez viszont azt is jelenti, hogy az $\langle A\text{'}B\text{'}C\rangle$ egyazon nyílt félterébe esik $D$ és $O$. Összességében azt kaptuk, hogy $D$ benne van a $B\text{'}C$, $B\text{'}C\text{'}$ és $B\text{'}A\text{'}$ közös $B\text{'}$ kezdőpontú félegyenesek által meghatározott nyílt ,,térnyolcadban''. Ebből következik, hogy a $D\text{'}B\text{'}$ szakasz metszi az $ABCA\text{'}B\text{'}C\text{'}$ poliéder belsejét, amivel ellentmondásra jutottunk. 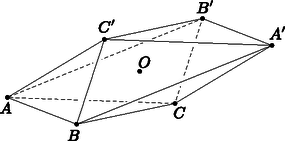    Ezzel az állítást beláttuk.