|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Az ábra jelöléseit használjuk. A két kérdéses átló és . Az hossza egyenlő a körülírt kör sugarával, -rel, így elegendő azt bizonyítanunk, hogy hossza is . Az pont a körülírt kör középpontja, így az szakasz hossza is . Azt fogjuk bizonyítani, hogy az háromszög egyenlőszárú. Húzzuk be az -hoz tartozó belső szögfelezőt, ez az ismert tétel szerint a körülírt körön metszi a szemben fekvő oldal felezőmerőlegesét. Legyen ez a pont . Ugyanez a szögfelező -ben metszi a szakaszt és két háromszögre osztja az háromszöget. A és az váltószög, mert és egyaránt merőlegesek a oldalra (oldalfelező merőleges és magasság), tehát a két szög egyenlő. Az háromszögben és egyaránt hosszúságúak, így a háromszög egyenlőszárú, tehát az alapon fekvő két szöge, és egyenlő. Eszerint a és az mindketten egyenlőek az szöggel, azaz egymással is egyenlőek. Ha az csúcshoz tartozó külső szögfelező párhuzamos -vel, akkor merőleges az -hoz tartozó belső szögfelezőre, azaz -re, mert az -beli külső és belső szögfelező merőlegesek egymásra. A és az is derékszög. Az és az háromszögekben az -nál és a -nél fekvő szögek nagysága is megegyezik, továbbá van egy közös oldaluk, a oldal, vagyis a két háromszög egybevágó. Az egybevágóság miatt és hossza megegyezik. Az szakasz hossza , így hossza is . Ezzel az állítást beláttuk.
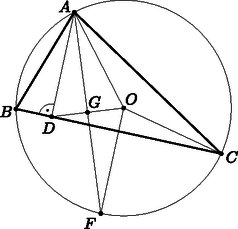
Megjegyzés. A konstrukció akkor is működik, ha , csak akkor a kérdéses négyszög konvex lesz, esetünkben pedig konkáv.
|
 PDF |
PDF |  MathML
MathML 