Feladat: B.4834 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Lukács Lilla Réka 
Füzet: 2017/április, 222. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Háromszögek egybevágósága, Síkgeometriai bizonyítások, Körülírt kör
Hivatkozás(ok):Feladatok: 2016/december: B.4834

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Használjuk az ábra jelöléseit. A K középpontú kör legyen k, az E és F középpontú körök pedig 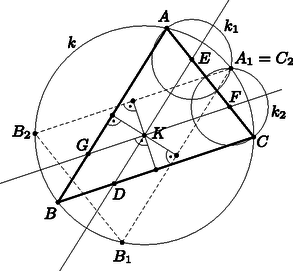k1 és k2.

 
 

A DE és FG egyenesek szimmetriatengelyei a háromszög körülírt körének, mivel átmennek a középpontján. Ugyanígy DE szimmetriatengelye a k1, FG pedig a k2 körnek.
Legyen az AB oldal DE-re vett tükörképe A1B1. Mivel A rajta van az AB egyenesen, a k és a k1 körön, a tükörképe, A1 is rajta van ezeken a körökön. Tehát a k és a k1 kör, valamint az A1B1 egyenes egy pontban metszik egymást és AB=A1B1.
Legyen a BC oldal FG-re vett tükörképe B2C2. Az előzőhöz hasonlóan, mivel a C pont rajta van a BC egyenesen, a k és a k2 körön, ezért tükörképe, C2 is rajta van ezeken a körökön. Tehát a k és a k2 kör, valamint a B2C2 egyenes egy pontban metszik egymást és BC=B2C2.
Két egymásra merőleges tengelyre való tükrözés a tengelyek metszéspontjára vonatkozó középpontos tükrözéssel egyenértékű. A B pont tengelyes tükörképe B1, ennek tükörképe pedig A1, ezért A1 a B pont középpontos tükörképe K-ra. Hasonlóan C2 is a B pont középpontos tükörképe K-ra.
Tehát A1=C2, vagyis a három kör egy pontban metszi egymást.