Feladat: B.4812 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 2017/március, 157 - 158. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai bizonyítások, Húrnégyszögek, Euler-egyenes, Magasságpont
Hivatkozás(ok):Feladatok: 2016/szeptember: B.4812

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.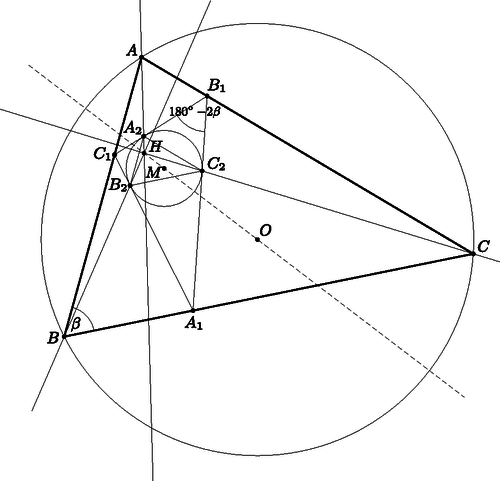

 
Megoldás. Használjuk az ábra jelöléseit. A Thalész-tétel megfordítása miatt BCB1C1 húrnégyszög, hiszen a BC szakasz a B1 és C1 pontokból is derékszög alatt látszik. Hasonlóan ABA1B1 és ACA1C1 is húrnégyszög. A húrnégyszög-tételt ABA1B1-ben, illetve BCB1C1-ben alkalmazva kapjuk, hogy A1B1A∢=180∘-β és C1B1C∢=180∘-β. Ezekből C1B1A∢=A1B1C∢=β adódik, amiből rögtön következik, hogy A1B1C1∢=180∘-2β, valamint hogy BB1 felezi az A1B1C1∢-et.

 
 

Hasonló megfontolásokkal kapjuk, hogy B1A1C∢=C1A1B∢=α, B1C1A∢=A1C1B∢=γ, és A1B1C1 belső szögei rendre 180∘-2α, 180∘-2β, 180∘-2γ, belső szögfelezői pedig éppen AA1, BB1 és CC1, az ABC háromszög magasságvonalai. Beláttuk tehát, hogy A1B1C1 beírt körének középpontja M, az ABC magasságpontja. Ebből azonnal következik, hogy A2, B2 és C2 éppen a beírt kör érintési pontjai A1B1C1 megfelelő oldalain, s így M az A2B2C2 körülírt körének középpontja is. Ismét a Thalész-tétel megfordítása és a húrnégyszög-tétel miatt A1C2MB2 húrnégyszög, hiszen B2 és C2 szögei derékszögek. Innen B2MC2∢=2α adódik, és kihasználva, hogy MB2C2 egyenlőszárú kapjuk, hogy MB2C2∢=MC2B2∢=90∘-α és C2B2A1∢=α. Ebből BA1B2∢=α miatt BC∥B2C2 adódik. Analóg módon beláthatjuk, hogy AB∥A2B2 és AC∥A2C2. Ezekből következik, hogy az ABC és A2B2C2 háromszögek hasonlóak, hiszen szögeik páronként megegyeznek.
Legyen H=AA2∩BB2. Az a H centrumú φ középpontos nagyítás, ami az A2B2 szakaszt AB-be viszi, képezze C2-t C*-ba. Mivel ABC▵∼A2B2C2▵∼ABC*▵, azért ABC▵≅ABC*▵, amiből C=C*, és így H∈CC2 következik. Ezzel az állítás első felét beláttuk, az AA2, BB2 és CC2 egyenesek a H pontban metszik egymást. Továbbá a φ középpontos nagyítás az A2B2C2 körülírt körének M középpontját ABC körülírt körének O középpontjába viszi, így H∈OM, vagyis H valóban illeszkedik ABC Euler-egyenesére.