Kezdőlap


Feladat:	B.4802	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andó Angelika , Borbényi Márton , Cseh Kristóf , Gáspár Attila , Horváth András János , Imolay András , Klász Viktória , Kocsis Júlia , Kővári Péter Viktor , Lajkó Kálmán , Matolcsi Dávid , Nagy Dávid Paszkál , Sudár Ákos , Tóth Viktor , Török Zsombor Áron , Váli Benedek , Várkonyi Dorka , Zólomy Kristóf
Füzet:	2016/december, 540 - 542. oldal		PDF \| MathML
Témakör(ök):	Feladat, Kúpok, Szabályos sokszögek geometriája, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 2016/május: B.4802

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Legyen $K$ csúcsa $C$ , a $G$ és a $g_{i}$ gömbök középpontja pedig $O$ , illetve $O_{i}$ $(i = 1,2, ..., n$ ). Vegyük $K$ metszetét a $C O O_{1}$ síkkal. Ez egy olyan egyenlőszárú $A B C$ háromszög, mely beírt körének középpontja $O$ és sugara $R$ , továbbá az $O_{1}$ középpontú $r$ sugarú kör érinti az $A B$ alapot, az $A C$ szárat és a beírt kört is (1. ábra). Legyen az $O_{1}$ -en átmenő, $A B$ -vel párhuzamos egyenes és a $C O$ egyenes metszéspontja $Q$ , az $O_{1} Q$ szakasz hosszát pedig jelöljük $d$ -ve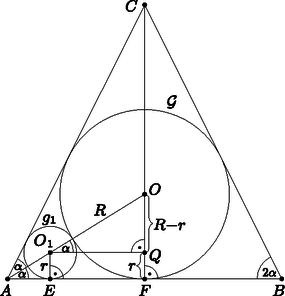l.

1. ábra

C A B ∢ = 2 α

, akkor

O A B ∢ = α

, mert a beírt kör középpontja rajta van a háromszög szögfelezőin. Mivel

O_{1} Q

párhuzamos

A B

-vel, ezért

Q

és

O_{1}

ugyanolyan távolságra van az

A B

egyenestől, amiből kapjuk, hogy

O Q = R - r

. Tudjuk, hogy egymást kívülről érintő körök esetén a két körközéppont távolsága megegyezik a körök sugarainak összegével, ezért

O O_{1} = R + r

. Az

O O_{1} Q

derékszögű háromszögből tehát egyrészt kapjuk, hogy

\begin{matrix} sin α = \frac{R - r}{R + r}, \end{matrix}

amiből (mivel

α < 90^{\circ}

, ezért sem itt, sem a későbbiekben nem áll nevezőben 0)

\begin{matrix} R = r \cdot \frac{1 + sin α}{1 - sin α}, azaz R + r = \frac{2 r}{1 - sin α}, \end{matrix}

majd ezt felhasználva:

\begin{matrix} O_{1} Q = d = (R + r) cos α = 2 r \cdot \frac{cos α}{1 - sin α} . \end{matrix}

A kétszeres szögekre vonatkozó trigonometrikus képleteket alkalmazva:

\begin{matrix} \frac{2 r}{d} = \frac{1 - sin α}{cos α} = \frac{{(cos \frac{α}{2} - sin \frac{α}{2})}^{2}}{cos^{2} \frac{α}{2} - sin^{2} \frac{α}{2}} = \frac{cos \frac{α}{2} - sin \frac{α}{2}}{cos \frac{α}{2} + sin \frac{α}{2}} = \frac{1 - tg \frac{α}{2}}{1 + tg \frac{α}{2}} = - 1 + \frac{2}{1 + tg \frac{α}{2}} . \end{matrix}

g_{1}, g_{2}, ..., g_{n}

gömbök középpontjai által alkotott

2 r

oldalú

O_{1} O_{2} ... O_{n}

szabályos

n

-szög síkja a kúp alapjával párhuzamos, attól

r

távolságra lévő sík. Mivel ebben a síkban

Q

is benne van és a gömbök szimmetrikus elhelyezkedése miatt

Q O_{i} = d

minden

i = 1,2, ..., n

esetén teljesül, ezért

Q

a szabályos sokszög köré írt kör középpontja. Legyen

φ = \frac{180^{\circ}}{n}

. Mivel a

Q O_{1} O_{2}

háromszög egyenlőszárú és szárszöge

2 φ

(2. ábra), ezért

\begin{matrix} sin φ = \frac{\frac{O_{1} O_{2}}{2}}{O_{1} Q} = \frac{r}{d} = \frac{1}{2} (- 1 + \frac{2}{1 + tg \frac{α}{2}}) . \end{matrix}

(1)

A B C

háromszög alapon fekvő szögei

2 α

nagyságúak, ezért

0^{\circ} < α < 45^{\circ}

. Tudjuk, hogy az

x \mapsto tg x

függvény a

[0, \frac{π}{4}]

intervallumon szigorúan monoton nő, ezért az

x \mapsto - 1 + \frac{2}{1 + tg x}

függvény ugyanitt szigorúan monoton csökken. Tehát (1)-ből azt kapjuk, hogy

\begin{matrix} \frac{1}{2} (- 1 + \frac{2}{1 + tg \frac{45^{\circ}}{2}}) < sin φ < \frac{1}{2} (- 1 + \frac{2}{1 + tg 0^{\circ}}) = \frac{1}{2} . \end{matrix}

(2)

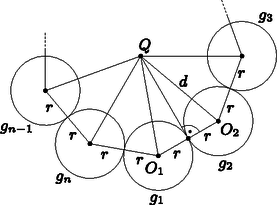2. ábra

A bal oldalon szereplő

tg \frac{45^{\circ}}{2}

értéket a 3. ábrán látható 1 befogójú egyenlőszárú derékszögű háromszöget felhasználva számoljuk ki. Mivel

A B = B C = 1

, ezért

A C = \sqrt[]{2}

. Ha az

A

-ból induló szögfelező a

B C

oldalt

D

-ben metszi, akkor egyrészt

B D = tg \frac{45^{\circ}}{2}

, másrészt a szögfelezőtétel szerint

B D / D C = A B / A C

, ebből pedig a

B D + D C = B C

összefüggést is figyelembe véve kapjuk, hogy

\begin{matrix} tg \frac{45^{\circ}}{2} = B D = \frac{A B \cdot B C}{A B + A C} = \frac{1}{1 + \sqrt[]{2}} = \sqrt[]{2} - 1. \end{matrix}

Ezért a (2) egyenlőtlenség bal oldalát átalakítva

\begin{matrix} sin φ > \frac{1}{2} (- 1 + \frac{2}{1 + (\sqrt[]{2} - 1)}) = \frac{\sqrt[]{2} - 1}{2} \end{matrix}

(3)

adódik. Tudjuk, hogy az

x \mapsto sin x

függvény is szigorúan monoton nő a

[0, \frac{π}{2}]

intervallumon, ezért a (2) és (3) egyenlőtlenségekből

φ = \frac{180^{\circ}}{n}

-re az alábbi korlátok adódnak:

\begin{matrix} arcsin \frac{\sqrt[]{2} - 1}{2} < \frac{180^{\circ}}{n} < arcsin \frac{1}{2}, azaz 11, 95^{\circ} < \frac{180^{\circ}}{n} < 30^{\circ}, \end{matrix}

vagyis

6 < n < 16

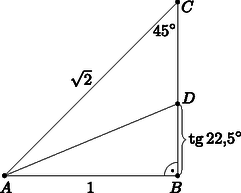3. ábra

Megmutatjuk, hogy az

n = 7,8, ...,15

értékekre léteznek is megfelelő kúpok. Az (1) egyenletből mindegyik

n

értékhez meghatározhatjuk a hozzá tartozó

α_{n}

szöget, ami az

n

-re vonatkozó egyenlőtlenségek miatt

0^{\circ}

-nál nagyobb, de

45^{\circ}

-nál kisebb lesz. Ezután pedig

r

ismeretében

R

is, s így a kúp is meghatározható.

Megjegyzés. Könnyen meggondolható, hogy

n = 6

esetén számolásunkból

R = r

adódik, azaz ebben az esetben a

R

sugarú gömb éppen ,,elfér'' a 6 db

r

sugarú gömb közt, nem magasodik ki közülük, ezért nem kapunk megfelelő kúpot. Ha pedig

n = 16

, akkor a

R

sugarú gömb ,,túlnyúlik'' a kis gömböket tartalmazó, középpontjaik síkjára merőleges alkotójú legszűkebb egyenes körhengeren, ezért nem kapunk megfelelő kúpot.