Feladat:	B.4774	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Barabás Ábel ,  Fülöp Anna Tácia
Füzet:	2016/december, 532 - 533. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Kúpszeletek érintői, Parabola egyenlete, Koordináta-geometria
Hivatkozás(ok):	Feladatok: 2016/február: B.4774

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A $p_1$ és a $p_3$ parabola metszéspontjának kiszámításához vonjuk ki $p_3$ egyenletéből $p_1$ egyenletét: $\begin{array}{c}{\displaystyle 0=2x^2+\left(b_3-b_1\right)x+\left(c_3-c_1\right)\mathrm{.}}\end{array}$ Ebből $\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}=\frac{-\left(b_3-b_1\right)\pm \sqrt[]{{\left(b_3-b_1\right)}^2-8\left(c_3-c_1\right)}}{4}\mathrm{.}}\end{array}$ A két parabola akkor érinti egymást, ha itt 0 a diszkrimináns, vagyis $\begin{array}{c}{\displaystyle {\left(b_3-b_1\right)}^2=8\left(c_3-c_1\right)\mathrm{.}}\end{array}$ (1) A metszéspont koordinátái ekkor: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x_1}& {\displaystyle =\frac{\left(b_1-b_3\right)}{4}\mathrm{,}}\hfill \\ \hfill {\displaystyle y_1}& {\displaystyle ={\left(\frac{\left(b_1-b_3\right)}{4}\right)}^2+b_3\frac{\left(b_1-b_3\right)}{4}+c_3\mathrm{.}}\hfill \end{array}}$ Hasonlóan a $p_2$ és a $p_3$ parabola esetében: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\left(b_3-b_2\right)}^2}& {\displaystyle =8\left(c_3-c_2\right)\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle x_2}& {\displaystyle =\frac{\left(b_2-b_3\right)}{4}\mathrm{,}}\hfill \\ \hfill {\displaystyle y_2}& {\displaystyle ={\left(\frac{\left(b_2-b_3\right)}{4}\right)}^2+b_3\frac{\left(b_2-b_3\right)}{4}+c_3\mathrm{.}}\hfill \end{array}}$ A két metszéspontot összekötő egyenes meredeksége: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m}& {\displaystyle =\frac{y_2-y_1}{x_2-x_1}=\frac{{\left(\frac{\left(b_2-b_3\right)}{4}\right)}^2+b_3\frac{\left(b_2-b_3\right)}{4}+c_3-{\left(\frac{\left(b_1-b_3\right)}{4}\right)}^2-b_3\frac{\left(b_1-b_3\right)}{4}-c_3}{\frac{\left(b_2-b_3\right)}{4}-\frac{\left(b_1-b_3\right)}{4}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{{\left(\frac{b_2-b_3}{4}\right)}^2-{\left(\frac{b_1-b_3}{4}\right)}^2+b_3\left(\frac{b_2-b_1}{4}\right)}{\frac{b_2-b_1}{4}}=\frac{\frac{{\left(b_2-b_3\right)}^2}{2}-\frac{{\left(b_1-b_3\right)}^2}{2}+2b_3\left(b_2-b_1\right)}{2\left(b_2-b_1\right)}\mathrm{.}}\hfill \end{array}}$ Az (1)-es és a (2) egyenlet felhasználásával ebből $\begin{array}{c}{\displaystyle m=\frac{4\left(c_1-c_2\right)-2b_3\left(b_1-b_2\right)}{2\left(b_2-b_1\right)}}\end{array}$ következik. A két parabolát egyszerre érintő egyenes egyenlete legyen $y=b_{0}x+c_0$. Ennek az egyenesnek akkor lesz egy közös pontja a parabolákkal, ha ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(b_0-b_1\right)}^2}& {\displaystyle =4\left(c_0-c_1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(b_0-b_2\right)}^2}& {\displaystyle =4\left(c_0-c_2\right)\mathrm{.}}\hfill \end{array}}$ Ebből: $\begin{array}{c}{\displaystyle b_0=\frac{-4\left(c_1-c_2\right)-\left(b_1^2-b_2^2\right)}{2\left(b_2-b_1\right)}\mathrm{.}}\end{array}$ Az (1)-es egyenletből kivonva a (2)-est: $\begin{array}{c}{\displaystyle b_1^2-b_2^2=-8\left(c_1-c_2\right)+2b_3\left(b_1-b_2\right)\mathrm{.}}\end{array}$ Ebből: $\begin{array}{c}{\displaystyle b_0=\frac{-4\left(c_1-c_2\right)+8\left(c_1-c_2\right)-2b_3\left(b_1-b_2\right)}{2\left(b_2-b_1\right)}=\frac{4\left(c_1-c_2\right)-2b_3\left(b_1-b_2\right)}{2\left(b_2-b_1\right)}\mathrm{.}}\end{array}$ Tehát $m=b_0$. Ezt kellett bizonyítani. 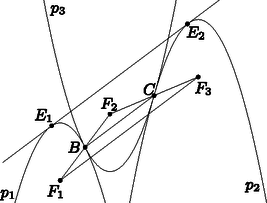  II. megoldás. Mivel a főegyütthatók megegyeznek vagy egymás ellentettjei, a három parabola egybevágó, és a vezéregyenesük párhuzamos az $x$ tengellyel. Az egymást érintő parabolák egymás középpontos tükörképei, ha a főegyütthatóik egymás ellentettjei. Ha ugyanis egy parabolát egy $P$ pontjára tükrözünk, akkor egy őt érintő parabolát kapunk: ha $P$-n kívül lenne más közös pontjuk, akkor annak a tükörképe is közös pont lenne, de három közös pontja nem lehet két különböző, függőleges tengelyű parabolának. Ha pedig az egyik parabola fókuszpontját az $y$ tengellyel párhuzamosan mozgatni kezdjük, akkor már nyilván nem lehet érintő.     Jelölje rendre $B$ és $C$ azt a két pontot, amiben $p_1$, illetve $p_2$ érinti $p_3$-at. A $p_1$-et és $p_2$-t úgy kaphatjuk meg, hogy $p_3$-at a $B$, illetve $C$ érintési pontra tükrözzük. Ebből következik, hogy a $p_1$ parabolának a $2\overrightarrow{BC}$ vektorral való eltoltja $p_2$. Ezért a $p_i$ parabolák $F_i$ fókuszaira is $\overrightarrow{F_1{F}_2}=2\overrightarrow{BC}$ teljesül. Jelölje végül $p_1$ és $p_2$ közös érintőjének e két parabolával vett érintési pontjait rendre $E_1$ és $E_2$. Ha az $E_1{E}_2$ egyenest eltoljuk $\overrightarrow{F_1{F}_2}$-vel, akkor a $p_2$-nek egy $E_1{E}_2$-vel párhuzamos érintőjét kapjuk. Mivel egy parabolának nincs két, egymással párhuzamos érintője, azért e két érintő egybeesik, azaz $E_1{E}_2$ párhuzamos $F_1{F}_2$-vel, az pedig párhuzamos az $F_1{F}_2{F}_3$ háromszög $F_1{F}_2$ oldalához tartozó középvonallal, $BC$-vel.