Feladat:	B.4716	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Andó Angelika ,  Kocsis Júlia ,  Kuchár Zsolt ,  Tóth Viktor
Füzet:	2016/április, 216 - 218. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai szerkesztések, Súlypont, Merőleges affinitás
Hivatkozás(ok):	Feladatok: 2015/május: B.4716

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Mindkét megoldás során fel fogjuk használni a következő, ismert állítást.   Lemma. Ha egy síkidomot két részre osztunk, a részek területei $T_1$ és $T_2$, súlypontjaik pedig $S_1$ és $S_2$, akkor a síkidom $S$ súlypontja az $S_1{S}_2$ szakasznak az a pontja, melyre $T_1:T_2=S_{2}S:S{S}_1$ teljesül.   Tudjuk, hogy a szabályos ötszög átlója párhuzamos az ötszög szemközti oldalával. Mivel a rombusz szemközti oldalai is párhuzamosak s egy adott ponton át egy adott egyenessel csak egy párhuzamos húzható, ezért $F$ megegyezik az $EC$ és $BD$ átlók metszéspontjával. Legyen a $BCDEF$ ötszöglemez súlypontja $S$. Ha a lemezt a $CD$ szakasz $f$ felezőmerőlegesével osztjuk két részre, akkor a részek $f$-re nézve szimmetrikusak, tehát súlypontjaik is azok, amiből a lemma miatt következik, hogy $S$ rajta van $f$-en. Osszuk most az ötszöglemezt az $EC$ egyenessel két részre. Az így keletkezett két háromszög, $BCF$ és $DEC$ egyenlőszárú, mert a rombusz oldalainak egyenlősége miatt $BF=AE$, tehát mindkét háromszögnek van két-két olyan oldala, melyek hossza megegyezik a szabályos ötszög oldalának hosszával. Legyen a $CF$, illetve $CE$ szakaszok felezőpontja $M_1$, illetve $M_2$, a $BCF$ és $DEC$ háromszögek súlypontja pedig $S_1$, illetve $S_2$ (1. ábra). Mivel bármely háromszögben a súlypont harmadolja a súlyvonalakat, ezért ekkor $S_1$ a $B{M}_1$, $S_2$ pedig a $D{M}_2$ szakasz $EC$ egyeneshez közelebbi harmadolópontja. Mivel a két háromszög egyenlő szárú, így $B{M}_1\perp CF$ és $D{M}_2\perp CE$. Ezért annál a merőleges tengelyes affinitásnál, melynek tengelye az $EC$ egyenes, aránya pedig $1/3$, a $B$ pont képe $S_1$, a $D$ pont képe $S_2$, a tengelyen lévő $F$ pont képe pedig önmaga lesz. Ezért az affinitásnál a $BFD$ egyenes képe az $S_{1}F{S}_2$ egyenes lesz, azaz $S_1{S}_2$ átme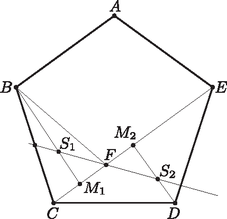gy $F$-en.   1. ábra   A lemma miatt a konkáv ötszöglemez súlypontja az $S_1{S}_2$ szakaszon is rajta van, tehát nem lehet más, mint $f$ és $S_1{S}_2$ metszéspontja. Vagyis a $BCDEF$ konkáv ötszöglemez súlypontja az $F$ pont.   II. megoldás. Jelölje a szabályos ötszög köré írható kör középpontját $K$, az $ABFE$ rombusz átlóinak metszéspontját pedig $M$. A szimmetria miatt nyilvánvaló, hogy ezek a pontok egyúttal a szabályos ötszög, illetve a rombusz súlypontjai is. Ha tehát a $BCDEF$ konkáv ötszöglemez súlypontja $N$, akkor a lemma alapján $K$ az $MN$ szakasznak az a pontja, melyre $MK:KN=T_{BCDEF}:T_{ABFE}$ teljesül. A területek arányát könnyen meghatározhatjuk. Legyen a szabályos ötszög oldalának hossza $1$. Ismert, hogy ekkor átlóinak hossza $\left(\sqrt[]{5}+1\right)/2$. A szabályos ötszög minden szöge ${108}^{\circ }$, ezért a köréírható körben az oldalaihoz tartozó kerületi szög $\frac{{180}^{\circ }-{108}^{\circ }}{2}={36}^{\circ }$ (2. ábra). Egy háromszög területét két oldalából és az azok által bezárt szög szinuszából kiszámolva kapjuk, hogy 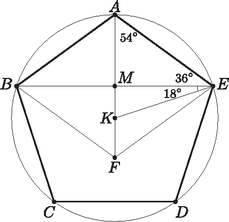${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABCDE}}& {\displaystyle =T_{AEB}+T_{BEC}+T_{CED}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\left(1\cdot \frac{\sqrt[]{5}+1}{2}\cdot \text{sin}{36}^{\circ }+{\left(\frac{\sqrt[]{5}+1}{2}\right)}^2\cdot \text{sin}{36}^{\circ }+1\cdot \frac{\sqrt[]{5}+1}{2}\cdot \text{sin}{36}^{\circ }\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{5+3\sqrt[]{5}}{4}\cdot \text{sin}{36}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{ABFE}}& {\displaystyle =2\cdot T_{AEB}=1\cdot \frac{\sqrt[]{5}+1}{2}\cdot \text{sin}{36}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{BCDEF}}& {\displaystyle =T_{ABCDE}-T_{ABFE}=\frac{5+3\sqrt[]{5}}{4}\cdot \text{sin}{36}^{\circ }-\frac{\sqrt[]{5}+1}{2}\cdot \text{sin}{36}^{\circ }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{3+\sqrt[]{5}}{4}\cdot \text{sin}{36}^{\circ }\mathrm{.}}\hfill \end{array}}$ Tehát $\begin{array}{c}{\displaystyle T_{BCDEF}:T_{ABFE}=\frac{3+\sqrt[]{5}}{2+2\sqrt[]{5}}=\frac{\sqrt[]{5}+1}{4}\mathrm{.}}\end{array}$ Az $AKE$ háromszög egyenlőszárú és szárszöge ${360}^{\circ }/5={72}^{\circ }$, tehát alapon fekvő szögei ${54}^{\circ }$-osak. Vagyis $\begin{array}{c}{\displaystyle MEK\sphericalangle =AEK\sphericalangle -AEM\sphericalangle ={54}^{\circ }-{36}^{\circ }={18}^{\circ }=\frac{MEF\sphericalangle }{2}\mathrm{,}}\end{array}$ ezért az $MEF$ háromszögben $EK$ szögfelező. Tehát a szögfelezőtétel szerint $\begin{array}{c}{\displaystyle \frac{MK}{KF}=\frac{ME}{EF}=\frac{\frac{\sqrt[]{5}+1}{4}}{1}=\frac{\sqrt[]{5}+1}{4}\mathrm{.}}\end{array}$   2. ábra   Vagyis az $F$ pontra teljesül, hogy $MK:KF=T_{BCDEF}:T_{ABFE}$, s mivel ilyen tulajdonságú pont csak egy van az $MK$ félegyenesen, ezért a lemmából következik, hogy a $BCDEF$ konkáv ötszöglemez súlypontja $F$.   Megjegyzés. Általában egy sokszöglemez súlypontja nem esik egybe a sokszög csúcsai által alkotott pontrendszer súlypontjával, ez csak háromszög esetén igaz. Erről részletesebben Bogdán Zoltánnak a B. 3295. feladathoz kapcsolódó cikkében1 és a Wikipedian2 olvashatunk. Azok a megoldók, akik a konkáv ötszöglemez csúcsaiba mutató vektorok számtani közepének segítségével próbálták meghatározni a lemez súlypontját, rossz megoldást adtak. 1Bogdán Zoltán: Megjegyzés a B. 3295. feladathoz ‐ alakzatok súlypontjáról, KöMaL, 50 (2000. február), 72‐75. http://db.komal.hu/KomalHU/cikk.phtml?id=200059. 2https://hu.wikipedia.org/wiki/Tömegközéppont.