Feladat:	B.4548	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Menyhért ,  Baran Zsuzsanna ,  Bingler Arnold ,  Csépai András ,  Emri Tamás ,  Fekete Panna ,  Gyulai-Nagy Szuzina ,  Janzer Barnabás ,  Janzer Olivér ,  Katona Dániel ,  Khayouti Sára ,  Kovács Márton ,  Makk László ,  Mezősi Máté ,  Mócsy Miklós ,  Nagy Gergely ,  Nagy-György Pál ,  Pap Tibor ,  Sagmeister Ádám ,  Sal Kristóf ,  Simkó Irén ,  Somogyvári Kristóf ,  Talyigás Gergely ,  Vető Bálint
Füzet:	2015/május, 275 - 277. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Háromszögek hasonlósága, Húrnégyszögek, Síkgeometriai számítások trigonometria nélkül, Esetvizsgálat
Hivatkozás(ok):	Feladatok: 2013/május: B.4548

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Az $A_1{B}_1{C}_1$ háromszög derékszögű csúcsa vagy valamelyik befogón vagy az átfogón van. I. eset: a derékszögű csúcs az átfogón található. Ekkor az $A_{1}B{B}_1{C}_1$ négyszög húrnégyszög, mivel szemközti szögeinek összege ${180}^{\ci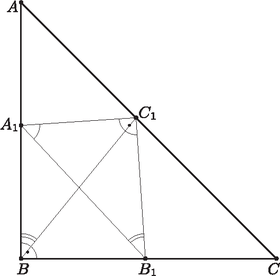rc }$ (1. ábra).   1. ábra   Az azonos húrhoz tartozó kerületi szögek egyenlők, így $A_{1}B{C}_1\sphericalangle =A_1{B}_1{C}_1\sphericalangle ={45}^{\circ }$, tehát az $ABC\sphericalangle$-et a $B{C}_1$ szakasz felezi. Mivel az $ABC$ háromszög egyenlő szárú, ezért ez a szögfelező egyben oldalfelező is, és így a $C_1$ pont az $AC$ szakasz felezőpontjában található (2. ábra). 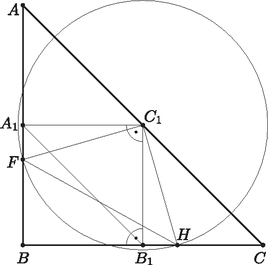  2. ábra   Legyen a $B_1$ pont a $BC$, az $A_1$ pont pedig az $AB$ oldal felezőpontja. Ekkor az $A_1{B}_1{C}_1$ és az $ABC$ háromszög közötti hasonlósági arány 1:2. Mivel $BC=1$, ezért $AC=\sqrt[]{2}$ és így $A_1{B}_1=\frac{\sqrt[]{2}}{2}$. Tekintsünk egy másik, $C_1$ csúcsú, egyenlő szárú derékszögű háromszöget. Mivel $C_1{B}_1\perp BC$, ezért ilyet csak úgy kapunk, ha egy $C_1$ középpontú, $r>C_1{B}_1$ sugarú körrel metsszük el az $ABC$ háromszög befogóit. A kapott háromszög befogója így nagyobb lesz, mint $C_1{B}_1$, és így nyilván az átfogója is nagyobb lesz, mint az $A_1{B}_1{C}_1$ háromszögé: $FH>A_1{B}_1$. Tehát ebben az esetben $A_1{B}_1$ minimuma $\frac{\sqrt[]{2}}{2}$. II. eset: a derékszögű csúcs az egyik befogón található. Legyen $A_1{B}_1=x$ és $B_{1}C=y$. Ekkor $A_1{C}_1=x\sqrt[]{2}$. Jelölje a $C{B}_1{C}_1$ szöget $\alpha$. Ekkor $C{C}_1{B}_1\sphericalangle ={180}^{\circ }-{45}^{\circ }-\alpha ={135}^{\circ }-\alpha$. Ebből $A{C}_1{A}_1\sphericalangle ={180}^{\circ }-C{C}_1{B}_1\sphericalangle -B_1{C}_1{A}_1\sphericalangle =\alpha$ és így $A{A}_1{C}_1\sphericalangle ={135}^{\circ }-\alpha$. Tehát a $B_{1}C{C}_1▵$ és a $C_{1}A{A}_1▵$ a szögei egyenlőek, ezért a két háromszög hasonló. Így 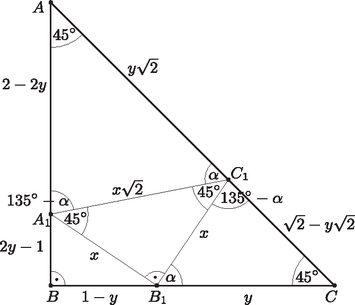$\begin{array}{c}{\displaystyle \frac{A{C}_1}{y}=\frac{x\sqrt[]{2}}{x}\mathrm{,}\text{amiből}A{C}_1=y\sqrt[]{2}\text{(<span style="font-style: italic;">3. ábra</span>).}}\end{array}$   3. ábra   Mivel $BC=1$, ezért egyrészt $B{B}_1=1-y$, másrészt $AC=\sqrt[]{2}$, és ebből $C{C}_1=\sqrt[]{2}-y\sqrt[]{2}$. Tudjuk, hogy $A{A}_1=\sqrt[]{2}C{C}_1$, amiből $A{A}_1=\sqrt[]{2}\left(\sqrt[]{2}-y\sqrt[]{2}\right)=2-2y$, és így $A_{1}B=1-\left(2-2y\right)=2y-1$. Az $A_{1}B{B}_1$ háromszögben felírhatjuk a Pitagorasz-tételt: $\begin{array}{c}{\displaystyle {\left(2y-1\right)}^2+{\left(1-y\right)}^2=x^2\mathrm{,}\text{vagyis}5y^2-6y+2=x^2\mathrm{.}}\end{array}$ Látható, hogy $x$-nek pontosan akkor van minimuma, amikor az $5y^2-6y+2$ kifejezésnek (ha a kifejezés értéke ott pozitív). Ennek a másodfokú függvénynek a minimumhelye $y=-\frac{b}{2a}=-\frac{-6}{2\cdot 5}=\frac{3}{5}$-ben van, ekkor $\begin{array}{c}{\displaystyle A_1{B}_1=x=\sqrt[]{5\cdot {\left(\frac{3}{5}\right)}^2-6\cdot \frac{3}{5}+2}=\frac{\sqrt[]{5}}{5}<\frac{\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Tehát az $A_1{B}_1$ távolság minimálisan $\frac{\sqrt[]{5}}{5}$ lehet.