Kezdőlap


Feladat:	B.4639	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter , Baran Zsuzsanna , Cseh Kristóf , Fekete Panna , Forrás Bence , Geng Máté , Győrfi -Bátori András , Gyulay-Nagy Szuzina , Kúsz Ágnes , Lajkó Kálmán , Nagy-György Pál , Schrettner Bálint , Simkó Irén , Williams Kada
Füzet:	2015/március, 155 - 157. oldal		PDF \| MathML
Témakör(ök):	Feladat, Ellipszis, mint mértani hely, Síkgeometriai bizonyítások, Érintőnégyszögek
Hivatkozás(ok):	Feladatok: 2014/május: B.4639

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.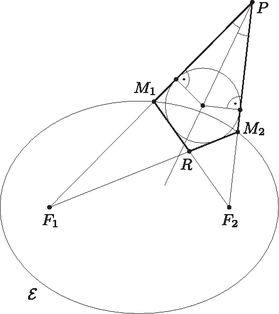

I. megoldás. Ha

P M_{1} R M_{2}

érintőnégyszög, akkor a beírható köre egyúttal az

F_{1} M_{2} P

háromszögnek és az

F_{2} M_{1} P

háromszögnek is beírható köre. Vizsgáljuk meg, hogy e két háromszögben a beírható kör a

P

csúcstól milyen távolságra érinti a

P

-n átmenő oldalakat. Ha e két távolság egyenlő, akkor a két kör egybeesik, mert az

F_{1} P F_{2}

szög szárait a szög csúcsától adott távolságra érintő kör egyértelműen létezik, középpontja a szög száraira az adott távolságban állított merőlegesek metszéspontja, sugara pedig e metszéspontnak a száraktól való távolsága (1. ábra).

1. ábra

Ismert, hogy ha egy háromszög oldalai

a, b

és

c

, akkkor a beírt kör oldalakon lévő érintési pontjainak a csúcsoktól való távolsága rendre

(a + b - c) / 2

(b + c - a) / 2

és

(c + a - b) / 2

. (Ennek bizonyítását a 2. ábra alapján az olvasóra bízzuk, csak annyit kell felhasználni, hogy külső pontból egy körhöz húzott két érintő hossza megegyezik.)

2. ábra

F_{1} M_{2} P

háromszög beírt köre tehát

P

-től

\frac{P F_{1} + P M_{2} - F_{1} M_{2}}{2}

, az

F_{2} M_{1} P

háromszög beírt köre pedig

P

-től

\frac{P F_{2} + P M_{1} - F_{2} M_{1}}{2}

távolságra érinti az

F_{1} P F_{2}

szög szárait. Megmutatjuk, hogy e két távolság egyenlő. Ehhez elegendő azt belátnunk, hogy

\begin{matrix} P F_{1} + P M_{2} - F_{1} M_{2} = P F_{2} + P M_{1} - F_{2} M_{1}, \end{matrix}

azaz

\begin{matrix} (P M_{1} + M_{1} F_{1}) + P M_{2} - F_{1} M_{2} = (P M_{2} + M_{2} F_{2}) + P M_{1} - F_{2} M_{1} \end{matrix}

teljesül. Ezt rendezve kapjuk, hogy elegendő megmutatnunk az

\begin{matrix} M_{1} F_{1} + F_{2} M_{1} = M_{2} F_{2} + F_{1} M_{2} \end{matrix}

egyenlőség fennállását, ami viszont azonnal következik abból, hogy

M_{1}

és

M_{2}

rajta vannak az

F_{1}

és

F_{2}

fókuszú

E

ellipszisen.
Tehát az

F_{1} M_{2} P

és az

F_{2} M_{1} P

háromszögek beírható körei egybeesnek, így ez a kör érinti a

P M_{1} R M_{2}

négyszög minden oldalát, ezért

P M_{1} R M_{2}

érintőnégyszög.

II. megoldás. A megoldás során felhasználjuk a kúpszeletek két tulajdonságát. A következő két lemma bizonyítása megtalálható pl. lapunk egy korábbi cikkében (Kiss Gy.: Amit jó tudni a kúpszeletekről, I. és II. rész, KöMaL 54. évf. (2004), 450‐459¹ és 514‐519²; 8, illetve 11. tétel).

1. lemma. A

K

kúpszelet tetszőleges

G

pontjában az érintő felezi a

G

-hez tartozó vezérsugarak szögét (3. ábra).

2. lemma. Ha egy külső

P

pontból érintőket húzunk a kúpszelethez, akkor a

P

-t az érintési pontokkal összekötő szakaszok a kúpszelet fókuszából vagy egyenlő, vagy pedig egymást

180^{\circ}

-ra kiegészítő szögekben látszanak. Az utóbbi eset csak hiperbolánál fordul elő (3. ábra).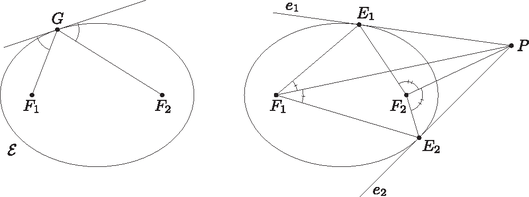

3. ábra

Legyen

i = 1,2

esetén

E

érintője az

M_{i}

pontban

e_{i}

, a két érintő metszéspontja pedig

K

(4. ábra). Ekkor az 1. lemma szerint

e_{1}

felezi a

P M_{1} F_{2} ∢

-et,

e_{2}

pedig a

P M_{2} F_{1} ∢

-et, mert az

E

-n lévő

M_{i}

ponthoz tartozó vezérsugarak

F_{1} M_{i}

és

F_{2} M_{i}

. A 2. lemmából pedig

M_{1} F_{2} K ∢ = M_{2} F_{2} K ∢

, valamint

M_{1} F_{1} K ∢ = M_{2} F_{1} K ∢

következik, mert a

K

pontból

E

-hez húzott

K M_{1}

és

K M_{2}

érintőszakaszok

E

fókuszaiból egyenlő szögekben látszanak. Tehát a

P M_{1} F_{2}

háromszögben

K M_{1}

és

K F_{2}

belső szögfelezők, ezért a háromszög beírható körének középpontja

K

. Bármely háromszögben a szögfelezők egy ponton mennek át, ezért

K P

felezi az

F_{1} P F_{2} ∢

-et. Ugyanígy kapjuk, hogy a

P M_{2} F_{1}

háromszög beírható körének középpontja is

K

, a

P M_{2} F_{1} ∢

-et felezi

M_{2} K

4. ábra

K

pont tehát a

P M_{1} R M_{2}

négyszög

M_{1}

M_{2}

és

P

csúcsából induló belső szögfelezőjén is rajta van, ezért a négyszög mind a négy oldalegyenesétől való távolsága ugyanaz az

r

érték. A

P M_{1} R M_{2}

négyszög nyilván konvex, ezért a

K

körül rajzolt

r

sugarú kör a négyszög mind a négy oldalszakaszát belső pontban érinti. Ezzel beláttuk, hogy

P M_{1} R M_{2}

érintőnégyszög.

¹http://www.komal.hu/cikkek/2004-11/kupszeletek1.h.shtml.

²http://www.komal.hu/cikkek/2004-12/kupszeletek2.h.shtml.