Kezdőlap


Feladat:	2015. évi Nemzetközi Fizika Diákolimpia 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2015/november, 491 - 494. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Atomreaktor
Hivatkozás(ok):	Feladatok: 2015/október: 2015. évi Nemzetközi Fizika Diákolimpia 3. feladata, 1984/november: F.2494, 1984/november: Gy.2225

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rész. Az üzemanyagrúd
A.1. A magreakció során felszabaduló energiát a tömegdefektusból számolhatjuk:

\begin{matrix} Δ E = [m (^{235} U) + m (^{1} n) - m (^{94} Zr) - m (^{140} Ce) - 2 m (^{1} n)] c^{2} . \end{matrix}

Összevonás után, a tömegek felhasználásával kapjuk:

\begin{matrix} Δ E = [m (^{235} U) - m (^{94} Zr) - m (^{140} Ce) - m (^{1} n)] c^{2} = 208, 7 MeV . \end{matrix}

A.2. Az

U_{2} O

(feladatban megadott) sűrűsége a térfogategységre eső molekulák össztömegét jelenti, így ezt elosztva a moláris tömeggel, majd megszorozva az

N_{A}

Avogadro-állandóval, megkapjuk az 1

m^{3}

-nyi anyagban található

U_{2} O

-molekulák

N_{1}

számát:

\begin{matrix} N_{1} = \frac{ϱ N_{A}}{M} = 2, 364 \cdot 10^{28} m^{- 3} . \end{matrix}

Az urán-dioxid molekuláknak azonban csak

0, 72 %

-a tartalmazza a 235-ös uránizotópot, így a feladat kérdésére a válasz:

\begin{matrix} N = 0, 0072 \cdot N_{1} = 1, 702 \cdot 10^{26} m^{- 3} . \end{matrix}

A.3. Az üzemanyagrúd egységnyi térfogatában

N

hasadó uránatom van, ezek teljes hatáskeresztmetszete

N σ_{f}

. Ha ezt megszorozzuk a

φ

neutronfluxussal, az időegység alatt (köbméterenként) bekövetkező hasadások számát kapjuk:

φ N σ_{f}

. Minden magreakcióban az A.1. részben kiszámolt

Δ E

energia szabadul fel, melynek

80 %

-a alakul hővé, így a hőfejlődés

Q

üteme:

\begin{matrix} Q = 0, 8 φ N σ_{f} Δ E = 4, 92 \cdot 10^{8} W / m^{3} . \end{matrix}

A.4. A

T_{c} - T_{s}

hőmérsékletkülönbség

K

dimenziójú, így az

F (Q, a, λ)

mennyiség mértékegysége is kelvin kell hogy legyen. Keressük az ismeretlen függvényt

F (Q, a, λ) = Q^{α} a^{β} λ^{γ}

alakban, és vizsgáljuk meg, mekkorának kell választanunk az

α, β, γ

számokat, hogy kelvin dimenziójú mennyiséget kapjunk. A jobb oldalon szereplő mennyiségek mértékegysége:

\begin{matrix} [Q] = W m^{- 3} = kg s^{- 3} m^{- 1}, [a] = m, [λ] = W m^{- 1} K^{- 1} = kg s^{- 3} m K^{- 1} . \end{matrix}

Ezek felhasználásával az alábbi egyenletet kapjuk a kitevőkre:

\begin{matrix} K = {(kg s^{- 3} m^{- 1})}^{α} m^{β} {(kg s^{- 3} m K^{- 1})}^{γ}, \end{matrix}

amiből

α = 1

β = 2

γ = - 1

adódik. Tehát az üzemanyagrúd közepének és felületének hőmérsékletkülönbségét megadó formula (a feladatban megadott

1 / 4

-es faktort is visszaírva)²:

\begin{matrix} T_{c} - T_{s} = \frac{Q a^{2}}{4 λ} . \end{matrix}

A.5. Az üzemanyagrúd közepének a hőmérséklete nem érheti el az

U_{2} O

olvadási hőmérsékletét, míg a külső felületének hőmérséklete a hűtőközeg hőmérsékletével egyezik meg. Így az A.4. részfeladatban kapott összefüggés szerint az üzemanyagrúd sugarának lehetséges legnagyobb

a_{u}

értéke

\begin{matrix} a_{u} = \sqrt[]{\frac{4 λ (T_{c} - T_{s})}{Q}}, \end{matrix}

ahol most

T_{c} = T_{olv} = 3138 K

T_{s} = 577 K

. A megadott adatokat és

Q

fentebb kiszámolt értékét behelyettesítve

a_{u} = 8, 27 \cdot 10^{- 3} m

B rész. A moderátor
B.1. Az ábrán láthatóak a sebességviszonyok a tömegközépponti koordináta-rendszerben. Fontos megjegyezni, hogy a

ϑ

szög nagyobb, mint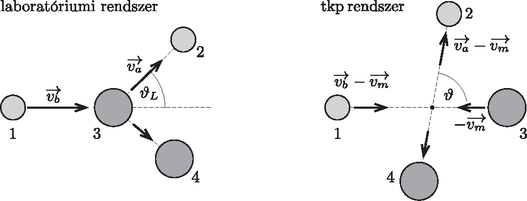

ϑ_{L}

B.2. A tömegközéppont sebessége a rendszer impulzusának és a teljes tömegének hányadosa:

\begin{matrix} v_{m} = \frac{v_{b}}{A + 1} . \end{matrix}

Ugyanekkora sebességgel mozog a tkp rendszerből nézve a laboratóriumi rendszerben kezdetben álló moderátoratom is:

\begin{matrix} V = \frac{v_{b}}{A + 1} . \end{matrix}

A neutron sebességének nagysága az ütközés előtt a tkp rendszerben:

\begin{matrix} v = v_{b} - v_{m} = \frac{A}{A + 1} v_{b} . \end{matrix}

A tkp rendszerben a rugalmas ütközés során az energia- és impulzusmegmaradás úgy teljesül, hogy a neutron és a moderátoratom is megőrzi az ütközés előtti sebességének nagyságát (rendre

v

és

V

), csupán a sebesség iránya változik meg.
B.3. Ütközés után a neutron sebességvektora a laboratóriumi rendszerben

\vec{v_{a}} = \vec{v} + \vec{v_{m}}

, így a sebességnégyzetének nagysága (a vektorháromszögben felírható koszinusztételből):

\begin{matrix} v_{a}^{2} = v^{2} + v_{m}^{2} + 2 v v_{m} cos ϑ . \end{matrix}

Behelyettesítve

v

és

v_{m}

előző részfeladatban kiszámolt értékét:

\begin{matrix} v_{a}^{2} = \frac{A^{2} v_{b}^{2}}{{(A + 1)}^{2}} + \frac{v_{b}^{2}}{{(A + 1)}^{2}} + \frac{2 A v_{b}^{2}}{{(A + 1)}^{2}} cos ϑ, \end{matrix}

amiből

\begin{matrix} G (α, ϑ) = \frac{E_{a}}{E_{b}} = \frac{v_{a}^{2}}{v_{b}^{2}} = \frac{A^{2} + 2 A cos ϑ + 1}{{(A + 1)}^{2}} . \end{matrix}

Ez kis átalakítással felírható

α

segítségével is:

\begin{matrix} G (α, ϑ) = \frac{A^{2} + 1}{{(A + 1)}^{2}} + \frac{2 A}{{(A + 1)}^{2}} cos ϑ = \frac{1}{2} [(1 + α) + (1 - α) cos ϑ] . \end{matrix}

B.4. Az energiaveszteség akkor a legnagyobb, ha a

G (α, ϑ)

mennyiség a lehető legkisebb. Ez (akár intuícióval, akár az előző részben kapott kifejezést vizsgálva) akkor következik be, ha

ϑ = 180^{\circ} = π

, azaz ha az ütközés lineáris. Ekkor

G (α, π) = α

, a legnagyobb relatív energiaveszteség pedig

\begin{matrix} f_{l} = {(\frac{E_{b} - E_{a}}{E_{b}})}_{{max}_{}^{}} = 1 - G (α, π) = 1 - α . \end{matrix}

Most

α = {(19 / 21)}^{2}

, így

f_{l} \approx 0, 181

C rész. A nukleáris reaktor
C.1. A reaktor térfogata adott:

V = π R^{2} H

. Kérdés, hogyan kell megválasztani az

R : H

arányt, hogy az elszökő neutronfluxusban szereplő

\begin{matrix} x = {(\frac{2, 405}{R})}^{2} + {(\frac{π}{H})}^{2} \end{matrix}

kifejezés minimális legyen. Fejezzük ki

R^{2}

értékét a térfogattal:

\begin{matrix} x = \frac{2, 405^{2} π H}{V} + {(\frac{π}{H})}^{2} . \end{matrix}

Bontsuk az első tagot két egyenlő kifejezés összegére, majd alkalmazzuk a számtani és mértani közepek között fennálló egyenlőtlenséget:

\begin{matrix} x = \frac{2, 405^{2} π H}{2 V} + \frac{2, 405^{2} π H}{2 V} + \frac{π^{2}}{H^{2}} \geq \sqrt[3]{\frac{2, 405^{2} π H}{2 V} \cdot \frac{2, 405^{2} π H}{2 V} \cdot \frac{π^{2}}{H^{2}}} . \end{matrix}

A jobb oldalon láthatóan kiesik

H

, így egy konstans értéket kapunk. Ezt a bal oldali kifejezés akkor veszi fel, ha a benne szereplő három tag értéke megegyezik, azaz

\begin{matrix} \frac{2, 405^{2}}{2 R^{2}} = \frac{π^{2}}{H^{2}}, valamint x = \frac{3 π^{2}}{H^{2}} . \end{matrix}

Használjuk még fel, hogy stacionárius állapotban az időegység alatt kiszökő és a láncreakcióban termelődő (többlet)neutronok száma megegyezik, vagyis

k_{1} x ψ = k_{2} ψ,

amiből

\begin{matrix} H = \sqrt[]{\frac{3 π^{2}}{x}} = \sqrt[]{\frac{3 π^{2} k_{1}}{k_{2}}} \approx 5, 87 m, és R = \frac{2, 405 H}{\sqrt[]{2} π} \approx 3, 175 m . \end{matrix}

C.2. A

d = 0, 287 m

oldalélű négyzetrácsba rendezett üzemanyag-kazetták mindegyikére

d^{2}

nagyságú keresztmetszet-terület jut a reaktorban. Mivel a reaktor teljes keresztmetszete

π R^{2}

(ahol

R

az előző feladatrészben meghatározott érték), így a reaktorban elférő kazetták száma legfeljebb

\begin{matrix} F_{n} = \frac{π R^{2}}{d^{2}} \approx 387. \end{matrix}

Egyetlen (henger alakú) fűtőkazetta térfogata

π r_{kazetta} H

(ahol

r_{kazetta} = 3, 617 \cdot 10^{- 2} m

), sűrűsége adott (

ϱ = 1, 060 kg m^{- 3}

), így a fűtőelemek össztömege

\begin{matrix} M = F_{n} π r_{kazetta} H ϱ \approx 9, 90 \cdot 10^{4} kg . \end{matrix}

²A dimenzióanalízis módszere egy dimenziótlan szorzótényező erejéig határozatlanul hagyja a megoldást. A helyzetet az tette volna egyértelművé, ha a feladat szövegében megadják, hogy a fizikai mennyiségek hatványainak szorzata előtt álló állandó számértéke éppen 1/4 (‐ a szerk.).