Feladat: B.4586 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Adorján Dániel ,  Fonyó Viktória ,  Jenei Adrienn ,  Kosztolányi Kata ,  Páli Petra 
Füzet: 2014/december, 530 - 531. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai bizonyítások, Húrnégyszögek, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 2013/december: B.4586

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az ABC háromszög szögeit a szokásos módon α, β, γ-val, az egymással egyenlő KL és LC szakaszok hosszát pedig t-vel. Ekkor KL∥BC miatt KLA∢=BCA∢ (egyállású szögek) és a feladat feltétele szerint LMB∢=BAC∢=α. Ezt figyelembe véve LMC∢=18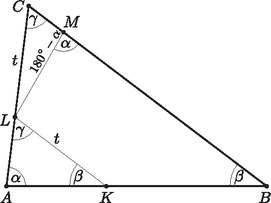0∘-LMB∢=180∘-α (1. ábra).


 

1. ábra
 

Az AKL és LMC háromszögekre alkalmazva a szinusz-tételt: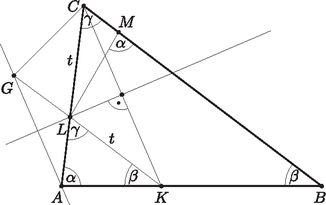
AK=KL⋅sinγsinα=t⋅sinγsinα,LM=LC⋅sinγsin(180∘-α)=t⋅sinγsinα.
A két egyenlőség alapján:
LM=AK.
 

 
II. megoldás. Tükrözzük az AKL háromszöget a CK szakasz felező merőlegesére. Ekkor az A pont tükörképe G és az ennél a csúcsnál lévő szög α (2. ábra). A CGLM négyszög olyan trapéz, amely egyben húrnégyszög is, mert a G és az M pontnál lévő szögei 180∘-ra egészítik ki egymást. Ezért a trapéz egyenlő szárú, tehát ML=CG=AK.


 

2. ábra
 

III. megoldás. Válasszuk meg a D pontot a BC egyenesen úgy, hogy DL=CL=LK=t legyen. Ekkor a DCL háromszög egyenlő szárú, így MDL∢=DCL∢=γ. Mivel DML∢=α, így az MLD háromszög harmadik szöge, 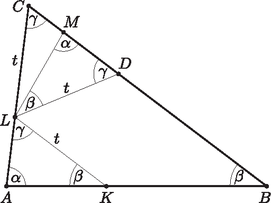MLD∢=β.


 

3. ábra
 

Mivel KL∥BC, ezért az AKL háromszög szögei is α, β és γ. Így az AKL és MLD háromszögek egybevágóak, mert KL=DL=t, és az ezen oldalakon lévő szögeik is egyenlők.
Az egybevágóság miatt a γ szöggel szemközti oldalaik is megegyeznek, így AK=LM.