Feladat:	B.4583	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Horeftos Leon ,  Kacz Dániel
Füzet:	2014/szeptember, 344 - 346. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Párhuzamos szelők tétele és megfordítása, Indirekt bizonyítási mód, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 2013/december: B.4583

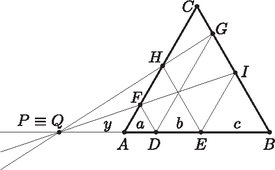
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha felcseréljük a $D$, $F$, $G$ pontok szerepét az $E$, $I$, $H$ pontokkal, az állítás önmagába megy át. Ezért az általánosság megszorítása nélkül feltehetjük, hogy $AD<AE$. Legyen $a=AD$, $b=DE$, $c=EB$. Ha $a=c$, akkor az $FI$ és a $GH$ egyenes is párhuzamos $AB$-vel, egyik sem metszi az $AB$-t. Legyen továbbá $FI$ és $AB$ metszéspontja $P$, $GH$ és $AB$ metszéspontja $Q$, az $AH$ és $BG$ metszéspontja pedig $C$. Szimmetria okokból feltehetjük, hogy $a<c$, így a $P$ és $Q$ pontok is a $BA$ félegyenes $A$-n túli meghosszabbításán helyezkednek el. Legyen még $PA=x$ és $QA=y$.     Az $AH$, $DG$ és $EI$ egyenesek párhuzamosak, mert az $AB$ egyenessel ${60}^{\circ }$-os szöget zárnak be. Alkalmazzuk a párhuzamos szelők tételét az $PAB$ és $PFI$ egyenesekre és az ezeket párhuzamosan metsző $AF$ és $EI$, illetve $FD$ és $IB$ egyenesekre: $\begin{array}{c}{\displaystyle \frac{PA}{PE}=\frac{PF}{PI}=\frac{PD}{PB}\mathrm{.}}\end{array}$ Most beírva az eddig jelölt szakaszokat: $\begin{array}{c}{\displaystyle \frac{x}{x+a+b}=\frac{x+a}{x+a+b+c}\mathrm{.}}\end{array}$ Innen a $PA$ szakasz $x$ hossza már kifejezhető: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x\left(x+a+b+c\right)}& {\displaystyle =\left(x+a\right)\left(x+a+b\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle x^2+ax+bx+cx}& {\displaystyle =x^2+ax+ax+a^2+bx+ab\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(c-a\right)x}& {\displaystyle =a\left(a+b\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle =\frac{a\left(a+b\right)}{c-a}\mathrm{.}}\hfill \end{array}}$ Most alkalmazzuk a párhuzamos szelők tételét a $QAB$ és $QHG$ egyenesekre és az ezeket párhuzamosan metsző $AH$, $EI$, illetve $EH$ és $BG$ egyenesekre is. $\begin{array}{c}{\displaystyle \frac{QA}{QD}=\frac{QH}{QG}=\frac{QE}{QB}\mathrm{.}}\end{array}$ A jelöléseinkkel pedig: $\begin{array}{c}{\displaystyle \frac{y}{y+a}=\frac{y+a+b}{y+a+b+c}\mathrm{.}}\end{array}$ Innen már azonnal adódik, hogy $\begin{array}{c}{\displaystyle y=\frac{a\left(a+b\right)}{c-a}=x\mathrm{.}}\end{array}$ A $P$ és $Q$ pontok megegyeznek, az $FI$ és $GH$ egyenesek az $AB$ egyenesen metszik egymást.     II. megoldás. Tartsuk meg az első megoldás ábrájának jelöléseit és az induló megjegyzéseket. Alkalmazzuk Meneleosz tételét az $ABC$ háromszögre és az $FI$ egyenesre: $\begin{array}{c}{\displaystyle \frac{CI}{IB}\cdot \frac{BP}{AP}\cdot \frac{AF}{FC}=1.}\end{array}$ Most beírva jelöléseinket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{a+b}{c}\cdot \frac{BP}{AP}\cdot \frac{a}{b+c}=\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{BP}{AP}=\frac{c\left(b+c\right)}{a\left(a+b\right)}\mathrm{.}}\hfill \end{array}}$ Alkalmazzuk Meneleosz tételét az $ABC$ háromszögre és a $GH$ egyenesre is: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{CG}{GB}\cdot \frac{BQ}{AQ}\cdot \frac{AH}{HC}=\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{a}{b+c}\cdot \frac{BQ}{AQ}\cdot \frac{a+b}{c}=\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{BQ}{AQ}=\frac{c\left(b+c\right)}{a\left(a+b\right)}\mathrm{.}}\hfill \end{array}}$ Látjuk, hogy $\begin{array}{c}{\displaystyle \frac{BP}{AP}=\frac{BQ}{AQ}\mathrm{,}}\end{array}$ a $P$ és $Q$ pontok megegyeznek.   Megjegyzés. A feladat projektív geometriai eszközökkel is megoldható. A megoldáshoz pontnégyesek kettősviszonyának tulajdonságait lehet felhasználni. A párhuzamos vetítések és az $\left(XYUV\right)=\left(YXVU\right)$ azonosság miatt $\begin{array}{c}{\displaystyle \left(ACFH\right)=\left(ABDE\right)=\left(CBGI\right)=\left(BCIG\right)\mathrm{.}}\end{array}$ Az $\left(A\mathrm{,}C\mathrm{,}F\mathrm{,}G\right)$ és a $\left(B\mathrm{,}C\mathrm{,}I\mathrm{,}G\right)$ pontnégyeseknek van közös pontja (a $C$ pont), ezért a két pontnégyes perspektív: az $AB\mathrm{,}FI$ és $HG$ egyenes (a projektív síkon) egy ponton megy át.