Kezdőlap


Feladat:	B.4542	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Maga Balázs
Füzet:	2014/május, 276 - 277. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Szögfelező egyenes, Középvonal, Párhuzamos szelők tétele és megfordítása
Hivatkozás(ok):	Feladatok: 2013/május: B.4542

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.

A háromszög három csúcsa legyen majd

A

B

és

C

,
A derékszög pedig forduljon az

A B

él fe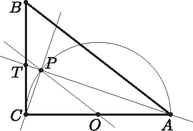lé.

A vizsgált szögfelező induljék teszem azt

A

-ból,
Ezzel semmit sem vonunk le az általánosságból.

Ez messe a

B C

oldalt a

T

-vel jelölt pontban,

C

A T

-re vetítettjének a

P

nevet adtam.

Ekkor

P

magasságtalppont

C A T

átfogóján,
Tehát

A T

belső pontja, ez evidens állítmány.

Mivel az

A P C

-ben

P

szöge 90 fokos,
Thalész szerint a köréírt körközpont

A C

-n tapos.

Vegyünk hát fel párhuzamost

A B

-vel

P

-n keresztül,
Ez elmetszi

A C

oldalt

O

-ban, valahol belül.

Legyen

C A B

szög

α

C O P

is ennyi lesz,
Feleennyit a

C A P

szög is ‐ én mondom ‐ kitesz.

Már csak egy sor van mi fontos, már csak ennyi kell ide:
A kerületi és középponti szögek tétele.

Hiszen így csakis

O

lehet

C A P

középpontja,
Minthogy egyrészt

A C

-n nyugszik, másrészt

C O P

α

Ennek pedig számunkra van egy szép következménye:

O

A C

felezőpontja, a középvonal vége.

Így mivel párhuzamos az

A B

oldallal

O P

P

a középvonalnak egy pontja, készen vagyunk, QED.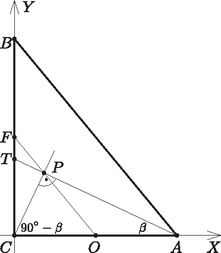

II. megoldás. Használjuk az I. megoldás jelöléseit, legyen továbbá

β = T A C ∢ = α / 2

. Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy annak

X

tengelye a

C A

, az

Y

tengelye a

C B

egyenes legyen, az egységet pedig válasszuk úgy, hogy az

A

pont koordinátái

(2; 0)

legyenek. Ekkor

T = (0; 2 tg β)

\begin{matrix} B = (0; 2 tg 2 β) = (0; \frac{4 tg β}{1 - tg^{2} β}) \end{matrix}

és a

C B

befogó

F

felezőpontjának koordinátái

\begin{matrix} (0, \frac{2 tg β}{1 - tg^{2} β}) . \end{matrix}

Mivel

P C O ∢ = 90^{\circ} - β

, azért a

C P

egyenes egyenlete

\begin{matrix} Y = tg (90^{\circ} - β) X = ctg β X, \end{matrix}

tehát

P = (p; p ctg β)

alakban írható. Az

A T

egyenes tengelymetszeti egyenlete

\begin{matrix} 1 = \frac{X}{2} + \frac{Y}{2 tg β}, \end{matrix}

erre illeszkedik a

P

pont, ezért

\begin{matrix} 1 = \frac{p}{2} + \frac{p ctg β}{2 tg β} = \frac{p}{2} (1 + \frac{1}{tg^{2} β}) . \end{matrix}

Ebből kapjuk, hogy

\begin{matrix} P = (\frac{2 tg^{2} β}{1 + tg^{2} β}; \frac{2 tg β}{1 + tg^{2} β}) . \end{matrix}

Feladatunk állításának igazolásához már csak azt kell megmutatnunk, hogy

P

koordinátái kielégítik az

O F

egyenes egyenletét. Ezt az egyenletet ismét a tengelymetszeteket felhasználva írhatjuk fel. Mivel

O = (1; 0)

, az egyenlet

\begin{matrix} 1 = \frac{X}{1} + \frac{Y}{\frac{2 tg β}{1 - tg^{2} β}} . \end{matrix}

Vagyis azt kell belátnunk, hogy

\begin{matrix} 1 = \frac{2 tg^{2} β}{1 + tg^{2} β} + \frac{\frac{2 tg β}{1 + tg^{2} β}}{\frac{2 tg β}{1 - tg^{2} β}} . \end{matrix}

Ez viszont azonnal adódik az emeletes tört egyszerűsítésével.