Kezdőlap


Feladat:	C.1072	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2013/január, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	C gyakorlat, Indirekt bizonyítási mód, Síkgeometriai bizonyítások, Beírt kör
Hivatkozás(ok):	Feladatok: 2011/március: C.1072

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B C$ derékszögű háromszögben ( $C$ a derékszög csúcsa) legyen $A C$ a hosszabbik befogó. A könnyebb számolás végett a $b$ oldal legyen egységnyi, a $B C = a$ befogó hossza $a \leq 1$ . Jelölje $O$ a beírt kör középpontját, amely az $A$ -ból és $C$ -ből induló szögfelezők metszéspontja.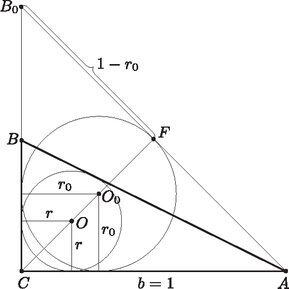
Tekintsük azt az egyenlő szárú derékszögű háromszöget, amelynek csúcsai $A$ , $C$ és $B_{0}$ , $B_{0} C = 1$ és $B_{0}$ a $C B$ félegyenesen van. A $C$ -ből induló szögfelező az $A C$ egyenessel $45^{\circ}$ -os szöget zár be. Messe ez az $A B_{0}$ oldalt az $F$ pontban. Legyen az $A B_{0} C$ háromszögbe írt kör középpontja $O_{0}$ .

Mivel

O

A B C

háromszög belsejében van, azért

O

rajta van a

C F

szakaszon. Az

A B C

háromszögbe írt kör

r

sugara kisebb, mint az

O_{0}

pontnak az

A C

egyenestől való távolsága, ami éppen az

A B_{0} C

háromszögbe írt kör

r_{0}

sugara.
Mivel

A C = B_{0} C = 1

A B_{0} = \sqrt[]{2}

. Az érintő szakaszok hosszának egyenlőségéből felírhatjuk, hogy

\begin{matrix} 1 - r_{0} + 1 - r_{0} = \sqrt[]{2}, és innen r_{0} = 1 - \frac{\sqrt[]{2}}{2} \approx 0, 293 < \frac{3}{10} . \end{matrix}

Pontosabban számolva: elég belátni, hogy

1 - \frac{\sqrt[]{2}}{2} \leq \frac{3}{10}

azaz

\frac{7}{5} \leq \sqrt[]{2}

, vagyis

7 \leq 5 \sqrt[]{2}

, négyzetre emelve

49 < 50

, ami igaz.

II. megoldás.

Ismeretes (és könnyen belátható), hogy a derékszögű háromszögbe írható kör

r

sugarára fennáll a következő egyenlőség:

r = \frac{a + b - c}{2}

Írjuk

c

helyébe a vele egyenlő

\sqrt[]{a^{2} + b^{2}}

-et:

\begin{matrix} r = \frac{a + b}{2} - \frac{\sqrt[]{a^{2} + b^{2}}}{2} . \end{matrix}

Felhasználva, hogy

\frac{a + b}{2} \leq \frac{\sqrt[]{a^{2} + b^{2}}}{\sqrt[]{2}}

(a számtani

és a négyzetes közép közötti egyenlőtlenség miatt), felírhatjuk, hogy

\begin{matrix} r \leq \frac{a + b}{2} - \frac{1}{\sqrt[]{2}} \frac{a + b}{2} \leq b (1 - \frac{1}{\sqrt[]{2}}) < \frac{3}{10} b, \end{matrix}

ahogy azt már az előbbi bizonyításban is láttuk.
Ezzel igazoltuk a feladat állítását.